 por phvicari » Sáb Fev 18, 2012 16:19
por phvicari » Sáb Fev 18, 2012 16:19
Olá, pessoal, estou com um exercício na mão aqui envolvendo função logarítimica, alguem poderia me ajudar com a parte inicial dele?
Aqui vai:
Considere a curva
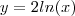
, onde "l" é a reta que passa pela origem e é tangente à curva no ponto "P". Considere também uma reta qualquer "m", perpendicular a "l" no ponto de tangencia "P".
Pergunta: Considerando que a cordenada x de P (Px) seja "t", o valor de

é?
PS: A resposta é que "t" vale

, portanto

é 1, mas não consigo de forma alguma chegar nesse valor para "t", alguem poderia me ajudar?
-
phvicari
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Set 03, 2011 04:25
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ensino Médio
- Andamento: cursando
 por LuizAquino » Sáb Fev 18, 2012 17:31
por LuizAquino » Sáb Fev 18, 2012 17:31
phvicari escreveu:Considere a curva

, onde "l" é a reta que passa pela origem e é tangente à curva no ponto "P". Considere também uma reta qualquer "m", perpendicular a "l" no ponto de tangencia "P".
Pergunta: Considerando que a cordenada x de P (Px) seja "t", o valor de ln (t) é?
Sabemos que a reta tangente a função f(x) no ponto P=(t, f(t)) é dada por:
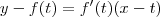
Como deseja-se que essa reta passe pela origem, o ponto x=0 e y=0 deve satisfazer essa equação. Ou seja, devemos ter:
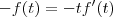
No exercício, temos que

. Lembrando que

, temos que a equação anterior será equivalente a:
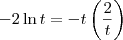
Agora tente terminar o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por phvicari » Sáb Fev 18, 2012 23:12
por phvicari » Sáb Fev 18, 2012 23:12
Professor LuizAquino, muito abrigado pela ajuda, consegui terminar o exercício e entendi perfeitamente a explicação.
Abraços.
-
phvicari
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Set 03, 2011 04:25
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ensino Médio
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Alguém pode me ajudar com este exercicio
por carvalhothg » Dom Set 04, 2011 18:40
- 1 Respostas
- 1754 Exibições
- Última mensagem por LuizAquino

Dom Set 04, 2011 20:19
Cálculo: Limites, Derivadas e Integrais
-
- Alguem pode me ajudar neste exercício, por favor...
por caducustodio » Sex Ago 17, 2012 09:00
- 1 Respostas
- 1815 Exibições
- Última mensagem por Cleyson007

Sex Ago 17, 2012 09:50
Sistemas de Equações
-
- Alguem pode ajudar não compreendi muito bem esse exercicio
por joaoalbertotb » Ter Set 01, 2009 14:08
- 11 Respostas
- 6722 Exibições
- Última mensagem por Elcioschin

Qui Set 03, 2009 17:02
Sistemas de Equações
-
- Alguem pode ajudar-me?
por carlos r m oliveira » Seg Out 05, 2009 11:35
- 1 Respostas
- 2544 Exibições
- Última mensagem por Neperiano

Dom Jul 03, 2011 21:05
Estatística
-
- Alguém pode me ajudar?
por apoliveirarj » Seg Jul 19, 2010 18:20
- 1 Respostas
- 3390 Exibições
- Última mensagem por Douglasm

Seg Jul 19, 2010 18:49
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
, onde "l" é a reta que passa pela origem e é tangente à curva no ponto "P". Considere também uma reta qualquer "m", perpendicular a "l" no ponto de tangencia "P".
é?
 , portanto
, portanto  é 1, mas não consigo de forma alguma chegar nesse valor para "t", alguem poderia me ajudar?
é 1, mas não consigo de forma alguma chegar nesse valor para "t", alguem poderia me ajudar?

 , onde "l" é a reta que passa pela origem e é tangente à curva no ponto "P". Considere também uma reta qualquer "m", perpendicular a "l" no ponto de tangencia "P".
, onde "l" é a reta que passa pela origem e é tangente à curva no ponto "P". Considere também uma reta qualquer "m", perpendicular a "l" no ponto de tangencia "P".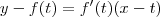
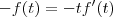
 . Lembrando que
. Lembrando que  , temos que a equação anterior será equivalente a:
, temos que a equação anterior será equivalente a: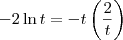

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
