Eu sei que é difícil responder e fdemorado fazer as respostas usando o editor de formulas mas eu preciso insistir nesse assunto, faz tempo que eu terminei os estudos (não lembro de mta coisa) e segundo me disseram é imprescindível que eu domine as fatorações se eu quiser avançar na matemática pq muitas coisas lá na frente vai ser necessário mta fatoração.
Então tenho 4 probleminhas aqui que deram um nó na cabeça e eu não consegui desenvolver.
1) Se
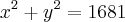 e
e  , calcule
, calcule  , sabendo que x e y são números positivos.
, sabendo que x e y são números positivos.Resposta : 49
2)Seja a expressão
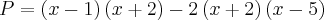
Se
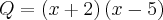 , simplifique o quociente
, simplifique o quociente 
Resposta :
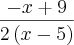
3)Simplifique a expressão
![E = {\left(\sqrt[]{28} - \sqrt[]{24} \right)}^{4} . {\left(\sqrt[]{28} + \sqrt[]{24} \right)}^{4 E = {\left(\sqrt[]{28} - \sqrt[]{24} \right)}^{4} . {\left(\sqrt[]{28} + \sqrt[]{24} \right)}^{4](/latexrender/pictures/83f876cf2318188e9fbc80c8003ac919.png)
Resposta : 64
4) Se x =
![\sqrt[]{3} + 1 \sqrt[]{3} + 1](/latexrender/pictures/ee55d11df65c893d0ddcfba13bff4395.png) , calcule
, calcule 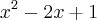
[/b]
Conto consigo



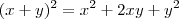 .
.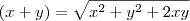 .
.
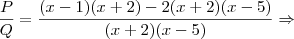
![\frac{P}{Q}=\frac{(x+2)[(x-1)-2(x-5)]}{(x+2)(x-5)} \Rightarrow \frac{P}{Q}=\frac{(x+2)[(x-1)-2(x-5)]}{(x+2)(x-5)} \Rightarrow](/latexrender/pictures/d5f8360a82c06c3668a18badd69c0fe9.png)
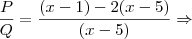
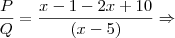
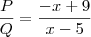
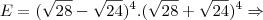
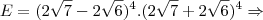
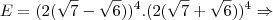
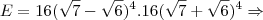
![E=256.[(\sqrt7-\sqrt6)(\sqrt7+\sqrt6)]^4 \Rightarrow E=256.[(\sqrt7-\sqrt6)(\sqrt7+\sqrt6)]^4 \Rightarrow](/latexrender/pictures/c9dfb953d065ab21e304edb0facca095.png)
![E=256.[(\sqrt7)^2-(\sqrt6)^2]^4 \Rightarrow E=256.[(\sqrt7)^2-(\sqrt6)^2]^4 \Rightarrow](/latexrender/pictures/f03510ece8213ab85afd9dfe29ea3e60.png)
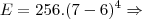
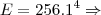


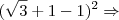
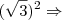

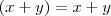
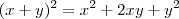
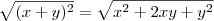
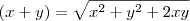

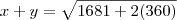
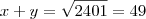
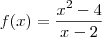
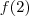 . Você não poderá pois a função retorna uma indeterminação... Neste caso, para determinar como a função se comporta próximo do ponto x=2, você deverá fazer uma simples manipulação, assim
. Você não poderá pois a função retorna uma indeterminação... Neste caso, para determinar como a função se comporta próximo do ponto x=2, você deverá fazer uma simples manipulação, assim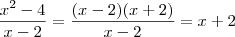
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
