 por ems » Sex Fev 22, 2008 17:47
por ems » Sex Fev 22, 2008 17:47
Se os termos da sequência (10,X,5) são inversamente proporcionais aos termos da sequência (20,50,Y), então:
a) X-Y=4
b) X+Y=40
c) X-Y=30
d) X+Y=54
e) X+Y=44
ALGUEM PODERIA ME AJUDAR COM ESTA QUESTÃO?
-
ems
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Fev 22, 2008 17:31
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Sex Fev 22, 2008 18:26
por admin » Sex Fev 22, 2008 18:26
Olá!
É preciso encontrar

e

.
Como os termos são inversamente proporcionais, podemos escrever a seguinte equação:
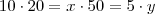
Repare que para manter a igualdade, sendo os termos inversamente proporcionais, se um aumentar, o outro precisa diminuir na mesma proporção.
Agora basta calcularmos

e

.
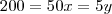
Dividindo por 5, temos:

Donde,

e



Portanto:
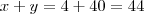
Alternativa (e).
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por ems » Sáb Fev 23, 2008 21:31
por ems » Sáb Fev 23, 2008 21:31
Valeu, muito obrigado pela ajuda.
-
ems
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Fev 22, 2008 17:31
- Área/Curso: Estudante
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- PRECISO DA RESPOSTA URGENTE
por trix17 » Qua Nov 09, 2011 23:34
- 0 Respostas
- 1392 Exibições
- Última mensagem por trix17

Qua Nov 09, 2011 23:34
Trigonometria
-
- Ajuda urgentemente
por luize » Qua Jul 04, 2012 18:48
- 1 Respostas
- 1471 Exibições
- Última mensagem por Russman

Qua Jul 04, 2012 19:38
Sistemas de Equações
-
- Função (Precisando urgentemente me encontrar neste assunto)
por adna » Qui Fev 20, 2014 00:11
- 3 Respostas
- 2271 Exibições
- Última mensagem por Russman

Seg Fev 24, 2014 00:10
Funções
-
- a sua resposta!!
por weverton » Seg Jul 12, 2010 18:44
- 1 Respostas
- 1368 Exibições
- Última mensagem por weverton

Seg Jul 12, 2010 19:22
Progressões
-
- Nao comsegui axa a resposta ...
por jean » Sáb Nov 29, 2008 17:44
- 2 Respostas
- 2023 Exibições
- Última mensagem por jean

Sáb Nov 29, 2008 21:45
Pedidos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 e
e  .
.
 e
e  .
.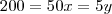





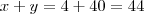




 , avisa que eu resolvo.
, avisa que eu resolvo.

