Estou encontrando dificuldade de interpretar qual é o grau do polinômio
 da questão que segue. Gostaria de saber o que devo fazer para encontrar o grau de
da questão que segue. Gostaria de saber o que devo fazer para encontrar o grau de  .
. --> Um polinômio
 é divisível por
é divisível por  e deixa resto 2 quando dividido por
e deixa resto 2 quando dividido por  . Calcule o resto da divisão de
. Calcule o resto da divisão de  por
por 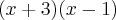 .
.Agradeço sua ajuda

Até mais.



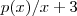




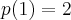

 da divisão de
da divisão de 

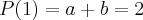 , pois o resto é
, pois o resto é  .
.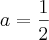
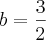
 .
.

 , avisa que eu resolvo.
, avisa que eu resolvo.

