homerbrasil escreveu:Sobre a segunda inequação, o gabarito deve estar errado mesmo, vi num site de matemática e me surpreendi de ter errado uma tão simples.
Com certeza esta errado... Você fez tudo certo.
homerbrasil escreveu:Sobre a primeira, ant_dii, entendi a sua explicação, há duas respostas

e

, e que deve-se considerar a segunda porque ela se "sobrepõe" na reta numérica

e
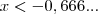
.
Na verdade a resposta que te dei não é
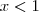
mas sim

(Me desculpe pois coloquei errado, acho que já estava cansado, afinal já era tarde). Por exemplo, se tomarmos

, veremos que

, ou seja,
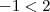
, o que é verdadeiro. Portanto você poderá tomar qualquer valor de

acima de 1 e também abaixo de -2/3.
O
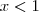
que apareceu e te (e me) confundiu foi para o caso em que tomaremos tanto o denominador como numerador negativos (isso quer dizer que a expressão é positiva).
Quanto
homerbrasil escreveu:Agora, sobre os conceitos de inequação. O que eu estava fazendo errado era passar uma expressão (

) que poderia ser negativa multiplicando o outro lado assumindo que ela era positiva. Como

pode assumir qualquer valor real exceto

a expressão seria negativa se
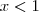
. E não se pode passar um número negativo multiplicando ou dividindo o outro lado da inequação. É isso mesmo? Algo a acrescentar?
na verdade o sinal não modifica quase nada... Veja, por exemplo:

.
Quanto a expressão

não poder ser zero, sim isso faz sentido, mas ao estudar cada caso (como fiz) você verá que o zero não esta no conjunto solução.
O cuidado deve ser tomado quando se tem
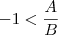
,
pois -1 é negativo, logo ou A é negativo e B positivo, ou A é positivo e B negativo.
Te peço atenção quanto as preposições
e e
ou.
Concluindo, eu errei na resposta do fim. O correto é o que esta entre chaves no fim, ou seja, o conjunto solução é
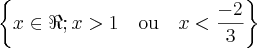
,
onde

é o conjunto dos números reais. Mil desculpas.
Só os loucos sabem...


![[(x+4)+(2x-2)]/(2x-2) > 0 [(x+4)+(2x-2)]/(2x-2) > 0](/latexrender/pictures/a1691fb69817ea246bdf77c50ca334fc.png)





 . Peço que vocês façam a resolução correta e me mostrem porque não consigo chegar no resultado.
. Peço que vocês façam a resolução correta e me mostrem porque não consigo chegar no resultado.


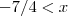 .
.




 multiplicando, pelo mesmo motivo
multiplicando, pelo mesmo motivo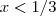

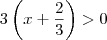 , de onde
, de onde 
 , de onde
, de onde  .
.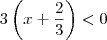 , de onde
, de onde 
 , de onde
, de onde 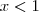 .
. é o conjunto
é o conjunto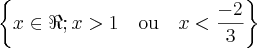 ,
, é o conjunto dos números reais.
é o conjunto dos números reais.
 e
e  , e que deve-se considerar a segunda porque ela se "sobrepõe" na reta numérica
, e que deve-se considerar a segunda porque ela se "sobrepõe" na reta numérica 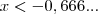 .
. , certo?
, certo? ) que poderia ser negativa multiplicando o outro lado assumindo que ela era positiva. Como
) que poderia ser negativa multiplicando o outro lado assumindo que ela era positiva. Como  pode assumir qualquer valor real exceto
pode assumir qualquer valor real exceto  a expressão seria negativa se
a expressão seria negativa se  , veremos que
, veremos que  , ou seja,
, ou seja, 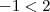 , o que é verdadeiro. Portanto você poderá tomar qualquer valor de
, o que é verdadeiro. Portanto você poderá tomar qualquer valor de  .
.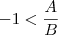 ,
,