Determine m e n

por **Cleyson007** » Qua Mai 20, 2009 13:28

Boa tarde!

Gostaria de saber se estou resolvendo corretamente a questão abaixo.

--> Calcule

e

reais para que $1+i\sqrt[2]{3}+\frac{m}{1+i\sqrt[2]{3}}=n$ .

Estou resolvendo assim: $({1+i\sqrt[2]{3}})^{2}+m=(1+i\sqrt[2]{3})(n)$

$(1+i\sqrt[2]{3})(1+i\sqrt[2]{3})+m=(1+i\sqrt[2]{3})(n)$

$1+i\sqrt[2]{3}+i\sqrt[2]{3}+{i}^{2}({\sqrt[2]{3}})^{2}+m=n+in\sqrt[2]{3}$

$1+2i\sqrt[2]{3}+(-3)+m=n(1+i\sqrt[2]{3})$

$1+2i\sqrt[2]{3}-3+m=n(1+i\sqrt[2]{3})$

$-2(1-i\sqrt[2]{3})+m=n(1+i\sqrt[2]{3})$

$-2(1-i\sqrt[2]{3})=n(1+i\sqrt[2]{3})-m$

$-2(\frac{1-i\sqrt[2]{3}}{1+i\sqrt[2]{3}})=n-m$

Estou encontrando essa equação: n=2+m

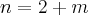
Agradeço sua ajuda :-D

Até mais

por **Molina** » Qua Mai 20, 2009 23:15

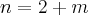
Cleyson007 escreveu: $-2(1-i\sqrt[2]{3})=n(1+i\sqrt[2]{3})-m$

$-2(\frac{1-i\sqrt[2]{3}}{1+i\sqrt[2]{3}})=n-m$

Essa passagem eu acho que não está certa.
Por que o $1+i\sqrt[2]{3}$ não está multiplicando todo o lado direito da igualdade para passar pro lado direito dividindo. Certo?

To meio sem tempo, mas vou ver aqui alguma coisa e qualquer novidade coloco aqui!

Bom estudo, :y:

por **Cleyson007** » Qui Mai 21, 2009 09:23

Bom dia Molina!

Molina, realmente... quando postei a questão no fórum não percebi esse meu erro :-D

Acho que o certo seria isolar a incógnita

e analisar os valores que atendem as condições (número real).

Obrigado pela ajuda.

Um abraço

por **-Tecno-** » Qui Mai 28, 2009 23:38

Oi Cleyson007! Me inscrevi no fórum agora para te responder e também participar desse fórum.

Eu comecei desde o início.

$1 + i\sqrt{3} + \frac{m}{1 + i\sqrt{3}} = n (1 + i \sqrt{3})^2 + m = n(1+i \sqrt{3}) 1 + 2i\sqrt{3} + 3(-1) + m = n + ni\sqrt{3} -2 + 2i\sqrt{3} + m = n + ni\sqrt{3} m - n - 2 + 2i\sqrt{3} - ni\sqrt{3} = 0 m - n - 2 + i(2\sqrt{3} - n\sqrt{3}) = 0$

Agora é que vem o pulo do gato. Esse zero é o mesmo que 0 + 0i

. Agora é só igualar a parte real com parte real e a imaginária com imaginária, tendo assim:

$m - n - 2 + i(2\sqrt{3} - n\sqrt{3}) = 0 + i0 2\sqrt{3} - n\sqrt{3} = 0 \Rightarrow n\sqrt{3} = 2\sqrt{3} n = 2 m - n - 2 = 0 \Rightarrow m = n + 2 m = 4$

Resposta:
m = 4