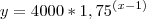por Tonga » Qui Jan 05, 2012 11:43
Bom dia,
Eu tenho algumas coordenadas de um plano (coordenadas abaixo) e preciso determinar uma função que passe por estes pontos.
A coordenada X é sequencial começando em 1, e Y é a incógnita.
Eu sei que esta função, é uma função exponecial do tipo
.
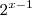A dúvida é, como devo proceder para determinar esta função ?
Coordenadas: (1,4000), (2,7000), (3,12250), (4,21437), (5,37515)
Obrigado.
-
Tonga
- Novo Usuário
-
- Mensagens: 2
- Registrado em: Qui Jan 05, 2012 11:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
por fraol » Qui Jan 05, 2012 16:29
Tonga,
Observando os seus dados, a gente vê cada
a partir do segundo é o anterior multiplicado por
.
Neste caso a gente tem uma PG cujo termo inicial é 4000 e a razão é
. Disso sai a equação que você procura, quer tentar?
-
fraol
- Colaborador Voluntário
-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
por Tonga » Qui Jan 05, 2012 18:28
Você está completamente certo !
A formula para ela seria
Muito Obrigado pela ajuda.
Mas infelismente eu coloquei os valores errados. Mil desculpas por isto.
Os valores corretos são:
Coordenadas: (1,8357), (2,14550), (3,20126), (4,25334), (5,30285)
O valor de Y continua sendo a incógnita e X um número inteiro, sequencial e maior que zero.
.
-
Tonga
- Novo Usuário
-
- Mensagens: 2
- Registrado em: Qui Jan 05, 2012 11:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Desafio: função real]Determinar a função f(x)
por raimundosar » Qui Mai 05, 2016 19:02
- 1 Respostas
- 2319 Exibições
- Última mensagem por nakagumahissao
Sex Mai 06, 2016 00:25
Funções
-
- Determinar a função
por yonara » Ter Jun 30, 2009 20:19
- 1 Respostas
- 3628 Exibições
- Última mensagem por Felipe Schucman
Seg Ago 03, 2009 21:15
Cálculo: Limites, Derivadas e Integrais
-
- determinar se é função
por virginia » Qui Abr 25, 2013 13:43
- 3 Respostas
- 1497 Exibições
- Última mensagem por e8group
Sex Abr 26, 2013 16:04
Funções
-
- [Função 1°grau] determinar função.
por Thiago 86 » Ter Abr 23, 2013 11:27
- 2 Respostas
- 2249 Exibições
- Última mensagem por Thiago 86
Ter Abr 23, 2013 13:05
Funções
-
- função. determinar o seno de y
por franciscokael » Qui Out 21, 2010 15:48
- 1 Respostas
- 1251 Exibições
- Última mensagem por MarceloFantini
Qui Out 21, 2010 18:15
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {
} e B = {
}, então o número de elementos A
B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {
} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {
} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
