![648\sqrt[2]{3} 648\sqrt[2]{3}](/latexrender/pictures/12eca2a634f48c8c9d9b150387089072.png) cm³, então o lado da base mede, em cm....
cm³, então o lado da base mede, em cm....Tenho pensando neste exercicio há uns dois dias, porém não consigo concluí-lo...
Primeiramente utilizo a formula do cálculo de volume de uma piramide, substituindo os dados do problema e obtenho a seguinte equação:

na proxima etapa de resolução, utilizo o valor do lado elevado ao quadrado na idéia da relação entre apótema e lado do hexagono regular:
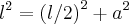
aí então recaio numa equação de terceiro grau e não concluo nada...
solicito e agradeço as ajudas prestadas
Cristina


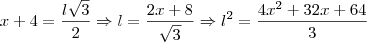
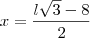
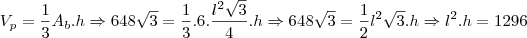
 e
e  teremos:
teremos: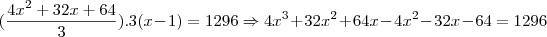

 é uma raiz do polinômio.
é uma raiz do polinômio.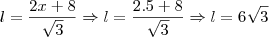


 .
.



