 por v0xxx » Sáb Dez 10, 2011 13:13
por v0xxx » Sáb Dez 10, 2011 13:13
Pensando numa solução pra um programa de computador cheguei a esta conclusão e funcionou perfeitamente. Mas gostaria de prová-la formalmente mas não tô conseguindo, se alguém ajudar eu agradeço. Segue a proposição:

Basicamente o que diz é: Se a soma do módulo de 2 números reais for menor que o módulo do 1º deles, então os números tem sinais contrários.
Como disse, está certo, mentalmente eu consigo provar, mas formalmente não consigo

-
v0xxx
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Dez 10, 2011 12:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Tecnologia da Informação
- Andamento: cursando
 por MarceloFantini » Dom Dez 11, 2011 04:00
por MarceloFantini » Dom Dez 11, 2011 04:00
Primeiro você quer dizer o módulo da soma, e não "soma do módulo de dois números reais", que seria algo como

. A condição de que tem sinais opostos pode ser simplificada para
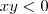
, ou seja, o produto é negativo.
Por último, não menos importante, um contra-exemplo: faça

e

. Então
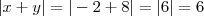
enquanto que

. Na verdade o que você provavelmente quer dizer é que se o módulo da soma for menor que o
máximo dentre os dois, então eles tem sinais opostos.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por v0xxx » Dom Dez 11, 2011 17:18
por v0xxx » Dom Dez 11, 2011 17:18
MarceloFantini escreveu:Primeiro você quer dizer o módulo da soma, e não "soma do módulo de dois números reais", que seria algo como

. A condição de que tem sinais opostos pode ser simplificada para
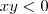
, ou seja, o produto é negativo.
Por último, não menos importante, um contra-exemplo: faça

e

. Então
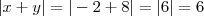
enquanto que

. Na verdade o que você provavelmente quer dizer é que se o módulo da soma for menor que o
máximo dentre os dois, então eles tem sinais opostos.
Exato, é o módulo da soma, eu me enganei. E de fato a lógica está um pouquinho errada. O certo certo é:
Se o módulo da soma for menor que o
maior deles em módulo então eles tem sinais contrários

(porque se fosse
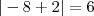
, que seria menor que
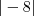
)
Muito obrigado!!!
-
v0xxx
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Dez 10, 2011 12:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Tecnologia da Informação
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- consigo na lógica mas na prática ta dificll
por Negte » Qui Fev 06, 2014 17:50
- 2 Respostas
- 1840 Exibições
- Última mensagem por Negte

Qui Fev 06, 2014 18:30
Álgebra Elementar
-
- [LÓGICA] simplificação lógica e leis de equivalência
por MatheusComp606 » Qua Ago 24, 2016 16:13
- 1 Respostas
- 5801 Exibições
- Última mensagem por adauto martins

Seg Ago 29, 2016 15:34
Lógica
-
- Pq será que não deu certo?
por Fernanda Lauton » Seg Jul 05, 2010 14:18
- 1 Respostas
- 1528 Exibições
- Última mensagem por Elcioschin

Seg Jul 05, 2010 15:06
Logaritmos
-
- L=R-C - Por favor, fiz certo ou não?
por HamiltonAN » Sex Jun 17, 2011 17:32
- 0 Respostas
- 1417 Exibições
- Última mensagem por HamiltonAN

Sex Jun 17, 2011 17:32
Álgebra Elementar
-
- Estou certo?
por Cleyson007 » Sáb Jun 09, 2012 13:01
- 1 Respostas
- 1539 Exibições
- Última mensagem por Molina

Sáb Jun 09, 2012 14:53
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






 . A condição de que tem sinais opostos pode ser simplificada para
. A condição de que tem sinais opostos pode ser simplificada para 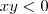 , ou seja, o produto é negativo.
, ou seja, o produto é negativo.  e
e  . Então
. Então 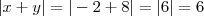 enquanto que
enquanto que  . Na verdade o que você provavelmente quer dizer é que se o módulo da soma for menor que o máximo dentre os dois, então eles tem sinais opostos.
. Na verdade o que você provavelmente quer dizer é que se o módulo da soma for menor que o máximo dentre os dois, então eles tem sinais opostos.

. A condição de que tem sinais opostos pode ser simplificada para
, ou seja, o produto é negativo.
e
. Então
enquanto que
. Na verdade o que você provavelmente quer dizer é que se o módulo da soma for menor que o máximo dentre os dois, então eles tem sinais opostos.
 (porque se fosse
(porque se fosse 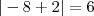 , que seria menor que
, que seria menor que 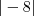 )
)
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
