 por matem » Sáb Dez 03, 2011 10:55
por matem » Sáb Dez 03, 2011 10:55
em uma pa de razão igual ao numero de termos , o primeiro e o ultimo termo são respectivamente 4 e 46.escreva a pa.
an=a1+(n-1)r
46=4+(46-1)r
46=4+45r
-45r=-46-4
-45r=-42???? está correto?
-
matem
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Seg Nov 28, 2011 18:04
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por matem » Sáb Dez 03, 2011 22:40
por matem » Sáb Dez 03, 2011 22:40
matem escreveu:em uma pa de razão igual ao numero de termos , o primeiro e o ultimo termo são respectivamente 4 e 46.escreva a pa.
an=a1+(n-1)r
46=4+(46-1)r
46=4+45r
-45r=-46-4
-45r=-42???? está correto?
por favor me ajudem a resolver
-
matem
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Seg Nov 28, 2011 18:04
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por TheoFerraz » Dom Dez 04, 2011 10:38
por TheoFerraz » Dom Dez 04, 2011 10:38
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por DanielFerreira » Sáb Jan 07, 2012 20:56
por DanielFerreira » Sáb Jan 07, 2012 20:56
matem escreveu:em uma pa de razão igual ao numero de termos , o primeiro e o ultimo termo são respectivamente 4 e 46.escreva a pa.
an=a1+(n-1)r
46=4+(46-1)r
46=4+45r
-45r=-46-4
-45r=-42???? está correto?

é o valor do
último termo.
n é a
quantidade de termos.
Não confunda!!
r = n
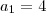


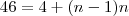
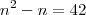

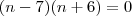
S = {- 6, 7}
Como o n° de termos não pode ser negativo,
n =
r = 7{4, 11, 18, 25, 32, 39, 46}"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (UNIFOR) Progressão Aritmética e Progressão Harmônica
por andersontricordiano » Ter Mar 22, 2011 12:56
- 1 Respostas
- 6139 Exibições
- Última mensagem por LuizAquino

Ter Mar 22, 2011 13:52
Progressões
-
- Progressão aritmética e progressão geométrica
por Danilo Dias Vilela » Sex Mar 12, 2010 13:41
- 1 Respostas
- 4730 Exibições
- Última mensagem por thadeu

Sex Mar 12, 2010 17:36
Progressões
-
- [Aritmética] Progressão Aritmética.
por Pessoa Estranha » Qua Ago 28, 2013 22:11
- 2 Respostas
- 5633 Exibições
- Última mensagem por Pessoa Estranha

Qui Ago 29, 2013 16:06
Aritmética
-
- Progressão Aritmética
por Rejane Sampaio » Qua Set 17, 2008 16:20
- 1 Respostas
- 4429 Exibições
- Última mensagem por juliomarcos

Qui Set 18, 2008 13:07
Álgebra Elementar
-
- Progressão Aritmética (PA)
por Cleyson007 » Ter Jan 27, 2009 21:40
- 2 Respostas
- 8406 Exibições
- Última mensagem por Cleyson007

Sáb Mai 30, 2009 12:31
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.








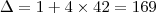
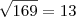


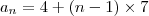

 é o valor do último termo.
é o valor do último termo.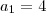


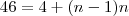
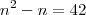

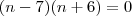


 .
.



