
Encontre a formula da derivada.
Eu fiz assim:

![\frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot \left(sin \left(\frac{x}{2}\right)\right)' \right] \frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot \left(sin \left(\frac{x}{2}\right)\right)' \right]](/latexrender/pictures/b714fc08b15c3e7cabbe23768d6ef967.png)
![\frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot cos\left(\frac{x}{2}\right)\cdot \left(\frac{x}{2}\right)' \right] \frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot cos\left(\frac{x}{2}\right)\cdot \left(\frac{x}{2}\right)' \right]](/latexrender/pictures/7adb9be375fc0eea770dd074e2c18f42.png)
![\frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot cos\left(\frac{x}{2}\right)\cdot \frac{2}{4} \right] \frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot cos\left(\frac{x}{2}\right)\cdot \frac{2}{4} \right]](/latexrender/pictures/137702bffa4660523cc604956e778581.png)
Será que está bem?Alguém pode conferir?
Isto de calcular a derivada complica-se quando é preciso misturar a regra do quociente, do produto e da cadeia.



![\frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot \left(sin \left(\frac{x}{2}\right)\right)' \right] \frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot \left(sin \left(\frac{x}{2}\right)\right)' \right]](/latexrender/pictures/b714fc08b15c3e7cabbe23768d6ef967.png)
![\frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot cos\left(\frac{x}{2}\right)\cdot \left(\frac{x}{2}\right)' \right] \frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot cos\left(\frac{x}{2}\right)\cdot \left(\frac{x}{2}\right)' \right]](/latexrender/pictures/7adb9be375fc0eea770dd074e2c18f42.png)
![\frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot cos\left(\frac{x}{2}\right)\cdot \frac{2}{4} \right] \frac{-2x}{x^4} \cdot sin^2 \left (\frac{x}{2} \right)+\frac{1}{x^2}\cdot \left [2 \cdot sin \left (\frac{x}{2}\right) \cdot cos\left(\frac{x}{2}\right)\cdot \frac{2}{4} \right]](/latexrender/pictures/137702bffa4660523cc604956e778581.png)

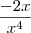 para
para 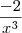 , não era necessário colocar
, não era necessário colocar  , embora não está errado a derivada de
, embora não está errado a derivada de  é
é  , não havia necessidade de multiplicar numerador e denominador por 2.
, não havia necessidade de multiplicar numerador e denominador por 2.  e então
e então  . Uma forma interessante seria notar que
. Uma forma interessante seria notar que  , daí
, daí 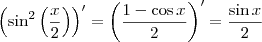 .
.  .
.

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes