 por mayara marangoni » Qui Nov 24, 2011 16:52
por mayara marangoni » Qui Nov 24, 2011 16:52
olá preciso de ajudar urgente para resolver duas questões de integral que não estou conseguindo terminar
1 -
![\int \frac{{e}^{\sqrt[]{x}}}{\sqrt[]{x}}dx \int \frac{{e}^{\sqrt[]{x}}}{\sqrt[]{x}}dx](/latexrender/pictures/c765464be2a37570a58c6ac136aff615.png)
e
2 [/tex]
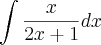
ajude-me
na segunda eu parei em
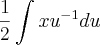
e na primeira parei em
2
Editado pela última vez por
mayara marangoni em Qui Nov 24, 2011 17:42, em um total de 2 vezes.
-
mayara marangoni
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Nov 24, 2011 16:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: eng ambiental
- Andamento: cursando
 por mayara marangoni » Qui Nov 24, 2011 16:57
por mayara marangoni » Qui Nov 24, 2011 16:57
na segunda eu parei em
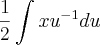
e na primeira parei em
2
-
mayara marangoni
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Nov 24, 2011 16:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: eng ambiental
- Andamento: cursando
 por mayara marangoni » Qui Nov 24, 2011 18:19
por mayara marangoni » Qui Nov 24, 2011 18:19
ALGUÉM ME AJUDA! ALI ONDE PAREI PODE FAZER INTEGRAÇÃO DIRETA?
-
mayara marangoni
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Nov 24, 2011 16:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: eng ambiental
- Andamento: cursando
 por TheoFerraz » Qui Nov 24, 2011 18:23
por TheoFerraz » Qui Nov 24, 2011 18:23
vamos resolver :
![\int_{}^{} \frac{{e}^{\sqrt[]{x}}}{\sqrt[]{x}} \int_{}^{} \frac{{e}^{\sqrt[]{x}}}{\sqrt[]{x}}](/latexrender/pictures/c82b10bb68a1b1ad55537f5ce7bb4b17.png)
vamos chamar
![\sqrt[]{x} = u \sqrt[]{x} = u](/latexrender/pictures/4a31029bf41b88b3a8587f4e6adaa748.png)
corrigindo os diferenciais, percebe-se que
![dx = 2 \; \sqrt[]{x} \times du dx = 2 \; \sqrt[]{x} \times du](/latexrender/pictures/22c73f1361b3aa7589864c84fe141bb2.png)
entao o que temos ?
![\int_{}^{} \frac{{e}^{u}}{u} 2 \; \sqrt[]{x} . du \int_{}^{} \frac{{e}^{u}}{u} 2 \; \sqrt[]{x} . du](/latexrender/pictures/88707131f7d50ad4237b9833e8b55198.png)
mas como
![\sqrt[]{x} = u \sqrt[]{x} = u](/latexrender/pictures/4a31029bf41b88b3a8587f4e6adaa748.png)
temos na verdade

isso voce sabe =)
agora a outra tente fazer algumas substituiçoes... tais como u = 2x + 1 ou algo do tipo... lembrando sempre que depois de voce corrigir os diferenciais, voce tem que manter TUDO em uma só variável... não faz NENHUM sentido ter "u's" e "X's" na mesma integral integrando du
Editado pela última vez por
TheoFerraz em Qui Nov 24, 2011 18:29, em um total de 1 vez.
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por TheoFerraz » Qui Nov 24, 2011 18:25
por TheoFerraz » Qui Nov 24, 2011 18:25
.
faça a substituição

lembrando sempre que voce pode usar isso como
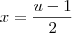
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por mayara marangoni » Qui Nov 24, 2011 19:23
por mayara marangoni » Qui Nov 24, 2011 19:23
Agora empaquei em integral de (u-1)/u du
-
mayara marangoni
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Nov 24, 2011 16:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: eng ambiental
- Andamento: cursando
 por mayara marangoni » Qui Nov 24, 2011 19:36
por mayara marangoni » Qui Nov 24, 2011 19:36
A resposta da 2 da -ln|1/2x+1|+K ?
-
mayara marangoni
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Nov 24, 2011 16:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: eng ambiental
- Andamento: cursando
 por LuizAquino » Qui Nov 24, 2011 23:17
por LuizAquino » Qui Nov 24, 2011 23:17
mayara marangoni escreveu:Agora empaquei em integral de (u-1)/u du
Aqui vai uma dica para auxiliar no estudo da resolução de uma integral.
Basta seguir os procedimentos abaixo.
- Acesse a página: http://www.wolframalpha.com/
- No campo de entrada, digite:
- Código: Selecionar todos
integrate (u-1)/u du
- Clique no botão de igual ao lado do campo de entrada.
- Após a integral ser calculada, clique no botão "Show steps" ao lado do resultado.
- Pronto! Agora basta estudar a resolução e comparar com a sua.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral de (e^2x)/x -- urgente!
por Moniky Ribeiro » Qui Jun 04, 2009 10:35
- 5 Respostas
- 16578 Exibições
- Última mensagem por ampat

Sáb Jun 27, 2009 09:52
Cálculo: Limites, Derivadas e Integrais
-
- INTEGRAL por partes [Urgente]
por LBT » Dom Out 31, 2010 23:49
- 11 Respostas
- 6901 Exibições
- Última mensagem por andrefahl

Qua Nov 03, 2010 14:26
Cálculo: Limites, Derivadas e Integrais
-
- Aplicações da Integral - URGENTE
por wweellddeerr » Seg Jun 27, 2011 16:05
- 0 Respostas
- 1193 Exibições
- Última mensagem por wweellddeerr

Seg Jun 27, 2011 16:05
Cálculo: Limites, Derivadas e Integrais
-
- Ajudas em integral (URGENTE)
por yuribam » Qua Nov 15, 2017 17:21
- 0 Respostas
- 3086 Exibições
- Última mensagem por yuribam

Qua Nov 15, 2017 17:21
Cálculo: Limites, Derivadas e Integrais
-
- INTEGRAL COM MÓDULO. ALGUEM ME AJUDA?URGENTE
 por nandafbb » Seg Nov 14, 2011 22:27
por nandafbb » Seg Nov 14, 2011 22:27
- 6 Respostas
- 3567 Exibições
- Última mensagem por MarceloFantini

Qui Nov 17, 2011 14:28
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 12 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int \frac{{e}^{\sqrt[]{x}}}{\sqrt[]{x}}dx \int \frac{{e}^{\sqrt[]{x}}}{\sqrt[]{x}}dx](/latexrender/pictures/c765464be2a37570a58c6ac136aff615.png)
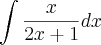
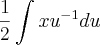


![\int \frac{{e}^{\sqrt[]{x}}}{\sqrt[]{x}}dx \int \frac{{e}^{\sqrt[]{x}}}{\sqrt[]{x}}dx](/latexrender/pictures/c765464be2a37570a58c6ac136aff615.png)
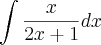
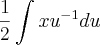


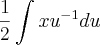



![\int_{}^{} \frac{{e}^{\sqrt[]{x}}}{\sqrt[]{x}} \int_{}^{} \frac{{e}^{\sqrt[]{x}}}{\sqrt[]{x}}](/latexrender/pictures/c82b10bb68a1b1ad55537f5ce7bb4b17.png)
![\sqrt[]{x} = u \sqrt[]{x} = u](/latexrender/pictures/4a31029bf41b88b3a8587f4e6adaa748.png)
![dx = 2 \; \sqrt[]{x} \times du dx = 2 \; \sqrt[]{x} \times du](/latexrender/pictures/22c73f1361b3aa7589864c84fe141bb2.png)
![\int_{}^{} \frac{{e}^{u}}{u} 2 \; \sqrt[]{x} . du \int_{}^{} \frac{{e}^{u}}{u} 2 \; \sqrt[]{x} . du](/latexrender/pictures/88707131f7d50ad4237b9833e8b55198.png)
![\sqrt[]{x} = u \sqrt[]{x} = u](/latexrender/pictures/4a31029bf41b88b3a8587f4e6adaa748.png) temos na verdade
temos na verdade


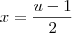




![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)