 por Raphael Feitas10 » Qua Nov 09, 2011 01:24
por Raphael Feitas10 » Qua Nov 09, 2011 01:24
Uma livraria pretende fazer seu balanço anual.Pedro e joão são os contabilistas da empresa.Se os dois trabalhassem juntos no serviço,eles fariam o balanço em 6 dias,porem,se joão trabalhar sozinho,realizará o serviço em 18 dias.Em quantos dias, pedro,trabalhando sozinho,concluirá o balanço? R:9
Brother eu interpretei ate aqui

mas ñ conseguie fazer ela me ajuda aew desde ja agradecido...
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por joaofonseca » Qua Nov 09, 2011 11:11
por joaofonseca » Qua Nov 09, 2011 11:11
Seja
y a velocidade a que Pedro trabalha,
x a velocidade a que João trabalha e
x+
y a velocidade a que os dois trabalham juntos. Seja
t a quantidade de trabalho a realizar.

Agora é uma questão de resolver o sistema, tendo em conta que x e y refletem a velocidade a que as pessoas trabalham.
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Raphael Feitas10 » Qua Nov 16, 2011 12:03
por Raphael Feitas10 » Qua Nov 16, 2011 12:03
brother fui resolvendo cheguei ate aqui
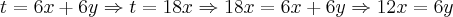
e ñ achei resposta nem uma me ajuda aew parceiro...
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por Raphael Feitas10 » Qui Nov 17, 2011 10:55
por Raphael Feitas10 » Qui Nov 17, 2011 10:55
Me ajuda aew galera por favor???
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Qui Nov 17, 2011 14:31
por MarceloFantini » Qui Nov 17, 2011 14:31
Raphael, procure prestar mais atenção. Se y é a velocidade que Pedro trabalha, o exercício pede para calcular

, e você encontrou que

, logo
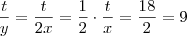
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por DanielFerreira » Sáb Abr 14, 2012 21:43
por DanielFerreira » Sáb Abr 14, 2012 21:43
Raphael Feitas10 escreveu:Uma livraria pretende fazer seu balanço anual.Pedro e joão são os contabilistas da empresa.Se os dois trabalhassem juntos no serviço,eles fariam o balanço em 6 dias,porem,se joão trabalhar sozinho,realizará o serviço em 18 dias.Em quantos dias, pedro,trabalhando sozinho,concluirá o balanço? R:9
Brother eu interpretei ate aqui

mas ñ conseguie fazer ela me ajuda aew desde ja agradecido...
Outra forma:
Tempo de Pedro: p
Tempo de João: j
Tempo total: Tt
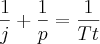
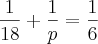




dias
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (UFRJ 2009 ) Questão do vestibular da ufrj em 2009 me ajudem
por rafael84 » Ter Jul 13, 2010 22:57
- 1 Respostas
- 2580 Exibições
- Última mensagem por Lucio Carvalho

Qui Jul 15, 2010 01:28
Binômio de Newton
-
- ANPEC-2009 Questão 14 - Integrais
por gjmiquel » Ter Nov 29, 2011 13:12
- 2 Respostas
- 1542 Exibições
- Última mensagem por gjmiquel

Qua Nov 30, 2011 09:14
Cálculo: Limites, Derivadas e Integrais
-
- Questão de concurso...
por henrivoador » Seg Abr 19, 2010 20:37
- 7 Respostas
- 11269 Exibições
- Última mensagem por henrivoador

Seg Abr 26, 2010 13:07
Logaritmos
-
- Questão de concurso
por bia rosendo » Qua Fev 23, 2011 11:00
- 4 Respostas
- 5787 Exibições
- Última mensagem por Elcioschin

Qui Fev 24, 2011 11:08
Funções
-
- Questão de concurso
 por bia rosendo » Seg Fev 28, 2011 22:54
por bia rosendo » Seg Fev 28, 2011 22:54
- 2 Respostas
- 7734 Exibições
- Última mensagem por LuizAquino

Ter Mar 01, 2011 14:12
Problemas do Cotidiano
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 mas ñ conseguie fazer ela me ajuda aew desde ja agradecido...
mas ñ conseguie fazer ela me ajuda aew desde ja agradecido...
 mas ñ conseguie fazer ela me ajuda aew desde ja agradecido...
mas ñ conseguie fazer ela me ajuda aew desde ja agradecido...


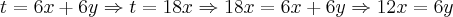 e ñ achei resposta nem uma me ajuda aew parceiro...
e ñ achei resposta nem uma me ajuda aew parceiro...

 , e você encontrou que
, e você encontrou que  , logo
, logo 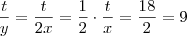 .
.

mas ñ conseguie fazer ela me ajuda aew desde ja agradecido...
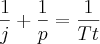
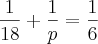



 dias
dias