Vitor2+ escreveu:QUESTÃO:
Determine, se possível, a equação geral do plano que contém o ponto A(1,2,1) e a reta interseção do plano ?:x-2y+z-3=0 com o plano yoz
Vitor2+ escreveu:RESOLUÇÃO
1) x=0
Ok. Este é o plano yOz.
Vitor2+ escreveu:2) x-2y+z-3=0 ? 0-2y+z-3=0 ? z=2y+3 (Equação da Reta)
Ok. Esta é a reta que é a interseção entre os planos x=0 e x-2y+z-3=0.
Vitor2+ escreveu:3) Utilizando as equações parametricas eu encontro um segundo ponto: P(0,0,3)
Ok. Mas note que a questão começa dizendo: "(...)
Determine, se possível (...)".
Quando
não seria possível determinar o plano que contém A=(1, 2, 1) e a reta z=2y+3 (que é interseção de x=0 e x-2y+z-3=0)?
Ora,
não seria possível caso o ponto A estivesse nessa reta. Entretanto, nesse caso o ponto A não está nessa reta, pois ele não está na interseção dos planos x=0 e x-2y+z-3=0. Note que esse ponto não pertence a nenhum desses planos!
Vitor2+ escreveu:4)

= P-A = (0,0,3) - (1,2,1) = (-1,-2,2). Chamarei esse vetor de vetor 2 (V2)
Ok.
Vitor2+ escreveu:5) Encontrar o vetor 1.
(a, b, c) ? (1, -2, 1)
Só não consigo encontrar os outros valores que (a, b, c) assumem para encontrar o vetor 1 (V1) e dar continuidade a questão.
Para determinar um plano, precisamos de três de seus pontos que não sejam colineares.
Você já sabe que A=(1, 2, 1) e P=(0, 0, 3) são dois pontos desse plano. Basta agora escolher qualquer outro ponto do plano que não seja colinear com A e P.
Para isso, basta escolher outro ponto da reta z=2y+3 (que é interseção de x=0 e x-2y+z-3=0). Por exemplo, escolha o ponto Q=(0, 1, 5).
Você sabe que os pontos A, P e Q não são colineares.
Basta agora determinar o vetor 1 como sendo

.
Vitor2+ escreveu:6) V1xV2=det

Fiquei travado neste ponto. Será que alguém pode me ajudar?
Basta continuar calculando:
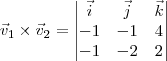
Vitor2+ escreveu:Como faço para achar a equação da reta interseção do plano com o plano yoz?
Mas você já encontrou! A reta z=2y+3 é a interseção entre os planos x=0 e x-2y+z-3=0.
ObservaçãoVitor2+ escreveu:6) V1xV2=det

Em matrizes, quando escrevemos os delimitadores com barras verticais, já estamos representando o determinante.
Por exemplo, considere a matriz:

Também poderíamos ter escrito essa matriz como:

Note que na primeira escrita usamos "[ ]" (colchetes) como delimitadores. Já na segunda escrita usamos "( )" (parênteses).
Para representar o determinante dessa matriz temos duas escritas básicas:
(i)

;
(ii)

(note que usamos "| |" -- barras verticais -- como delimitadores);
Não devemos escrever algo como:

Por outro lado, não teria problema ter escrito algo como:
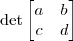
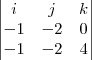 . Não pode ser nulo, pois, são linearmente independentes.
. Não pode ser nulo, pois, são linearmente independentes.  : -8x+4y+d = 0. Substituir o ponto A(1, 2, 1) na equação. -8.(1)+4.(2)+d=0. Sendo assim, d=0.
: -8x+4y+d = 0. Substituir o ponto A(1, 2, 1) na equação. -8.(1)+4.(2)+d=0. Sendo assim, d=0. : -8x+4y=0.
: -8x+4y=0.



 = P-A = (0,0,3) - (1,2,1) = (-1,-2,2). Chamarei esse vetor de vetor 2 (V2)
= P-A = (0,0,3) - (1,2,1) = (-1,-2,2). Chamarei esse vetor de vetor 2 (V2) .
.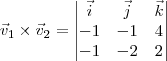


 ;
; (note que usamos "| |" -- barras verticais -- como delimitadores);
(note que usamos "| |" -- barras verticais -- como delimitadores);
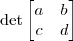

 .
.
 :
: