 por beel » Dom Set 11, 2011 15:09
por beel » Dom Set 11, 2011 15:09
![\lim_{x\rightarrow \infty}x(\sqrt[]{x^2-1} - x ) \lim_{x\rightarrow \infty}x(\sqrt[]{x^2-1} - x )](/latexrender/pictures/1443925313d565a0b1e9fef39c26fd83.png)
Meu resultado deu zero, mas estou muito em duvida...
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por beel » Dom Set 11, 2011 20:25
por beel » Dom Set 11, 2011 20:25
Nao entendi essa parte
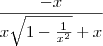
Voce colocou o x em evidencia? o que voce fez?
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Seg Set 12, 2011 01:00
por MarceloFantini » Seg Set 12, 2011 01:00
Sim, eu coloquei o x em evidência no denominador para cancelar com o numerador, usando que

quando x é positivo (que não precisamos nos preocupar já que está indo para infinito).
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por beel » Sáb Set 17, 2011 19:17
por beel » Sáb Set 17, 2011 19:17
o resultado nao seria negativo?
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por beel » Dom Out 16, 2011 16:59
por beel » Dom Out 16, 2011 16:59
Tudo bem,obrigada.
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limite] dúvida raíz
por beel » Dom Set 11, 2011 21:02
- 7 Respostas
- 3102 Exibições
- Última mensagem por beel

Qua Set 21, 2011 13:18
Cálculo: Limites, Derivadas e Integrais
-
- Limite - como resolver um lim quando temos raiz^2 e raiz^3.
por Monica santos » Sex Ago 16, 2013 14:22
- 4 Respostas
- 4131 Exibições
- Última mensagem por young_jedi

Sex Ago 16, 2013 19:01
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo: limite com raiz dentro de raiz
 por roberto_trebor » Sáb Fev 15, 2014 20:45
por roberto_trebor » Sáb Fev 15, 2014 20:45
- 1 Respostas
- 2240 Exibições
- Última mensagem por Man Utd

Dom Fev 16, 2014 17:58
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] raiz
por beel » Ter Set 06, 2011 13:48
- 5 Respostas
- 2607 Exibições
- Última mensagem por beel

Sex Set 09, 2011 16:52
Cálculo: Limites, Derivadas e Integrais
-
- Limite com Raiz
por Thyago Quimica » Sex Mai 25, 2012 18:08
- 1 Respostas
- 1390 Exibições
- Última mensagem por Guill

Sex Mai 25, 2012 20:03
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow \infty}x(\sqrt[]{x^2-1} - x ) \lim_{x\rightarrow \infty}x(\sqrt[]{x^2-1} - x )](/latexrender/pictures/1443925313d565a0b1e9fef39c26fd83.png)

![\lim_{x\rightarrow \infty}x(\sqrt[]{x^2-1} - x ) \lim_{x\rightarrow \infty}x(\sqrt[]{x^2-1} - x )](/latexrender/pictures/1443925313d565a0b1e9fef39c26fd83.png)


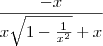

 quando x é positivo (que não precisamos nos preocupar já que está indo para infinito).
quando x é positivo (que não precisamos nos preocupar já que está indo para infinito).



