 por Thauan_Barcellos » Sex Out 14, 2011 16:27
por Thauan_Barcellos » Sex Out 14, 2011 16:27
Olá pessoal , estava fazendo esta questão :
(UFMG) Seja

-

, a>0 . O Valor da base a é :
a) 1/16
b) 1/8
c )2
d)10
e)16
Bom inicialmente eu tentei fazer isso :
a -

=8
1 -

= 8
Como que devo começar a fazer esta equação ?
-
Thauan_Barcellos
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Ago 20, 2011 11:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por TheoFerraz » Sex Out 14, 2011 16:58
por TheoFerraz » Sex Out 14, 2011 16:58
Sempre que voce estiver lidando com logarítimos, ao ver o seguinte termo matematico :

Leia em voz alta da seguinte forma: "Qual número 'c' que eu devo elevar a base 'a' de modo a resultar em 'b'
entao no seu caso:
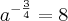
Pelas regras de potenciação:
![\frac{1}{\sqrt[4]{{a}^{3}}} = 8 \frac{1}{\sqrt[4]{{a}^{3}}} = 8](/latexrender/pictures/f0cde939070b58e0b239c197664615d4.png)
![\sqrt[4]{{a}^{3}} = \frac{1}{8} \sqrt[4]{{a}^{3}} = \frac{1}{8}](/latexrender/pictures/4fe474e926bcad56dfbccf717f7a6f59.png)
ou melhor

preferi escrever assim pq agora pra passar para o outro lado ficaria :
![a = {\left(\frac{1}{8} \right)}^{4/3} = \sqrt[3]{{\left(\frac{1}{8} \right)}^{4}} = \sqrt[3]{\frac{1}{4096}} = \frac{1}{16} a = {\left(\frac{1}{8} \right)}^{4/3} = \sqrt[3]{{\left(\frac{1}{8} \right)}^{4}} = \sqrt[3]{\frac{1}{4096}} = \frac{1}{16}](/latexrender/pictures/51be3713e6e94656a16bb48e4fc57a70.png)
Simples assim.
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por Thauan_Barcellos » Sex Out 14, 2011 17:08
por Thauan_Barcellos » Sex Out 14, 2011 17:08
Dúvida respondida , obrigado pela ajuda

-
Thauan_Barcellos
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Ago 20, 2011 11:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função Logarítmica
por OtavioBonassi » Qui Jan 06, 2011 21:58
- 12 Respostas
- 8061 Exibições
- Última mensagem por OtavioBonassi

Sex Jan 07, 2011 23:42
Funções
-
- Função Logaritmica
por nessitahfl » Qui Abr 17, 2014 11:06
- 3 Respostas
- 2592 Exibições
- Última mensagem por nessitahfl

Ter Abr 22, 2014 10:48
Funções
-
- Função Logarítmica
por Carlos28 » Sex Mar 13, 2015 10:02
- 2 Respostas
- 2471 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:36
Logaritmos
-
- Função logarítmica
por zenildo » Qua Jul 15, 2015 12:26
- 1 Respostas
- 2059 Exibições
- Última mensagem por nakagumahissao

Qui Jul 16, 2015 14:37
Logaritmos
-
- Função Logarítmica - Urgente!
por Asustek27 » Dom Mar 14, 2010 19:24
- 2 Respostas
- 2695 Exibições
- Última mensagem por Asustek27

Seg Mar 15, 2010 15:25
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 -
- , a>0 . O Valor da base a é :
, a>0 . O Valor da base a é : =8
=8 = 8
= 8
 -
- , a>0 . O Valor da base a é :
, a>0 . O Valor da base a é : =8
=8 = 8
= 8

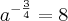
![\frac{1}{\sqrt[4]{{a}^{3}}} = 8 \frac{1}{\sqrt[4]{{a}^{3}}} = 8](/latexrender/pictures/f0cde939070b58e0b239c197664615d4.png)
![\sqrt[4]{{a}^{3}} = \frac{1}{8} \sqrt[4]{{a}^{3}} = \frac{1}{8}](/latexrender/pictures/4fe474e926bcad56dfbccf717f7a6f59.png) ou melhor
ou melhor 
![a = {\left(\frac{1}{8} \right)}^{4/3} = \sqrt[3]{{\left(\frac{1}{8} \right)}^{4}} = \sqrt[3]{\frac{1}{4096}} = \frac{1}{16} a = {\left(\frac{1}{8} \right)}^{4/3} = \sqrt[3]{{\left(\frac{1}{8} \right)}^{4}} = \sqrt[3]{\frac{1}{4096}} = \frac{1}{16}](/latexrender/pictures/51be3713e6e94656a16bb48e4fc57a70.png)





 , avisa que eu resolvo.
, avisa que eu resolvo.

