[quote="qrover"]
![\left(\frac{x^2+2x}{4} \right).\sqrt[2]{x^2+4} \left(\frac{x^2+2x}{4} \right).\sqrt[2]{x^2+4}](/latexrender/pictures/8c107f5833a8952777ab35c37e5a5dc9.png)
[quote]
aqui você usa a regra do produto:
![\left(\frac{x^2+2x}{4} \right).\frac{d}{dx}\sqrt[2]{x^2+4} + \sqrt[2]{x^2+4}.\frac{d}{dx}\left(\frac{x^2+2x}{4} \right) \left(\frac{x^2+2x}{4} \right).\frac{d}{dx}\sqrt[2]{x^2+4} + \sqrt[2]{x^2+4}.\frac{d}{dx}\left(\frac{x^2+2x}{4} \right)](/latexrender/pictures/0ca8879c5ba40a3537fed68a6ad062b1.png)
observer que neste trecho
![\frac{d}{dx}\sqrt[2]{x^2+4} \frac{d}{dx}\sqrt[2]{x^2+4}](/latexrender/pictures/77f778be584038b436b32a676a5ac56b.png)
você vai ter que usar a regra da cadeia:
então chamemos a função
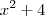
de g(x) e a função
![\sqrt[2]{x} \sqrt[2]{x}](/latexrender/pictures/2b552177173f128f54e48de06c7de3d9.png)
de f(x), então temos um f[g(x)]. a regra da cadeia diz que f[g(x)} é a derivada da função de de fora(
![\sqrt[2]{x} \sqrt[2]{x}](/latexrender/pictures/2b552177173f128f54e48de06c7de3d9.png)
) aplicada na função de dentro (
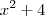
) multiplicada pela derivada da função de dentro (
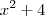
)
aplicando a regra da cadeia(vou chamar
![\sqrt[2]{x} \sqrt[2]{x}](/latexrender/pictures/2b552177173f128f54e48de06c7de3d9.png)
de

):
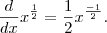
agora organizando, temos:
![\frac{1}{\sqrt[2]{x^2+4}} \frac{1}{\sqrt[2]{x^2+4}}](/latexrender/pictures/535e1c1ad7541b5335c9f6b92c9207b7.png)
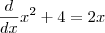
agora organizando, colocando g(x) dentro, temos:
![\frac{1}{\sqrt[2]{x^2+4}}.2x \frac{1}{\sqrt[2]{x^2+4}}.2x](/latexrender/pictures/c289b1613915fa2282e169b77b75cc59.png)
voltando à primeira parte do problema, fica assim a montagem:
![\left(\frac{x^2+2x}{4} \right).\frac{1}{\sqrt[2]{x^2+4}}.2x + \sqrt[2]{x^2+4}.\left(\frac{x}{2}+\frac{1}{2} \right) \left(\frac{x^2+2x}{4} \right).\frac{1}{\sqrt[2]{x^2+4}}.2x + \sqrt[2]{x^2+4}.\left(\frac{x}{2}+\frac{1}{2} \right)](/latexrender/pictures/caf5488f14f2d3fd0b1d74cf46421c50.png)
resolvido a primeira parte, temos que resolver a segunda ( não se esqueça de calcular o que eu não calculei na primeira parte):
![2ln(x+\sqrt[2]{x^2+4}) 2ln(x+\sqrt[2]{x^2+4})](/latexrender/pictures/04f50ce3e2cbe5df95ef9b1bb80f8f7a.png)
temos que derivar isso daí..
de novo temos uma regra da cadeia onde a função de fora é lnx e a de dentro
![(x+\sqrt[2]{x^2+4}) (x+\sqrt[2]{x^2+4})](/latexrender/pictures/5032e5aa1fd4b22994ef36cf5825ae82.png)
:
![2.\frac{1}{(x+\sqrt[2]{x^2+4})}.\frac{d}{dx}(x)+\sqrt[2]{x^2+4}) 2.\frac{1}{(x+\sqrt[2]{x^2+4})}.\frac{d}{dx}(x)+\sqrt[2]{x^2+4})](/latexrender/pictures/887de4766c2517843ea8090ff2ef4ae8.png)
( observe que você tem uma soma, então deve derivar um e outro:
![\frac{d}{dx}(x)+\frac{d}{dx}\sqrt[2]{x^2+4} \frac{d}{dx}(x)+\frac{d}{dx}\sqrt[2]{x^2+4}](/latexrender/pictures/3bd8b63c26a3b2ca933e51bb9f18bebb.png)
. só que neste ultimo trecho, você cai em outra regra da cadeia:
![\frac{d}{dx}\sqrt[2]{x^2+4} \frac{d}{dx}\sqrt[2]{x^2+4}](/latexrender/pictures/77f778be584038b436b32a676a5ac56b.png)
.
logo, a derivada completa ficaria como algo dessa forma:
![\left(\frac{x^2+2x}{4} \right).\frac{1}{\sqrt[2]{x^2+4}}.2x + \sqrt[2]{x^2+4}.\left(\frac{x}{2}+\frac{1}{2} \right)- 2.\frac{1}{(x+\sqrt[2]{x^2+4})}.\frac{d}{dx}(x)+\sqrt[2]{x^2+4}) \left(\frac{x^2+2x}{4} \right).\frac{1}{\sqrt[2]{x^2+4}}.2x + \sqrt[2]{x^2+4}.\left(\frac{x}{2}+\frac{1}{2} \right)- 2.\frac{1}{(x+\sqrt[2]{x^2+4})}.\frac{d}{dx}(x)+\sqrt[2]{x^2+4})](/latexrender/pictures/bff0c84c74856930c4bfe7465ecc39b3.png)
acredito que tenha esclarecido algo.. mas se os demais colegas encontrarem algum erro ou quiserem comentar, eu fico feliz, porque assim eu tbm aprendo mais..


![\left(\frac{x^2+2x}{4} \right).\sqrt[2]{x^2+4}-2lnx+\sqrt[2]{x^2+4} \left(\frac{x^2+2x}{4} \right).\sqrt[2]{x^2+4}-2lnx+\sqrt[2]{x^2+4}](/latexrender/pictures/7688f254b70cee12d5094ca6afa69f57.png)
![\left(\frac{x^2+2x}{4} \right).\sqrt[2]{x^2+4}-2ln(x+\sqrt[2]{x^2+4}) \left(\frac{x^2+2x}{4} \right).\sqrt[2]{x^2+4}-2ln(x+\sqrt[2]{x^2+4})](/latexrender/pictures/26da0748f444fcb7d3f0ff46d1548fe7.png)
![\left(\frac{x^2+2x}{4} \right).\sqrt[2]{x^2+4} \left(\frac{x^2+2x}{4} \right).\sqrt[2]{x^2+4}](/latexrender/pictures/8c107f5833a8952777ab35c37e5a5dc9.png)
![\left(\frac{x^2+2x}{4} \right).\frac{d}{dx}\sqrt[2]{x^2+4} + \sqrt[2]{x^2+4}.\frac{d}{dx}\left(\frac{x^2+2x}{4} \right) \left(\frac{x^2+2x}{4} \right).\frac{d}{dx}\sqrt[2]{x^2+4} + \sqrt[2]{x^2+4}.\frac{d}{dx}\left(\frac{x^2+2x}{4} \right)](/latexrender/pictures/0ca8879c5ba40a3537fed68a6ad062b1.png)
![\frac{d}{dx}\sqrt[2]{x^2+4} \frac{d}{dx}\sqrt[2]{x^2+4}](/latexrender/pictures/77f778be584038b436b32a676a5ac56b.png) você vai ter que usar a regra da cadeia:
você vai ter que usar a regra da cadeia: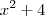 de g(x) e a função
de g(x) e a função ![\sqrt[2]{x} \sqrt[2]{x}](/latexrender/pictures/2b552177173f128f54e48de06c7de3d9.png) de f(x), então temos um f[g(x)]. a regra da cadeia diz que f[g(x)} é a derivada da função de de fora(
de f(x), então temos um f[g(x)]. a regra da cadeia diz que f[g(x)} é a derivada da função de de fora( ):
):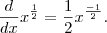 agora organizando, temos:
agora organizando, temos: ![\frac{1}{\sqrt[2]{x^2+4}} \frac{1}{\sqrt[2]{x^2+4}}](/latexrender/pictures/535e1c1ad7541b5335c9f6b92c9207b7.png)
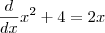
![\frac{1}{\sqrt[2]{x^2+4}}.2x \frac{1}{\sqrt[2]{x^2+4}}.2x](/latexrender/pictures/c289b1613915fa2282e169b77b75cc59.png)
![\left(\frac{x^2+2x}{4} \right).\frac{1}{\sqrt[2]{x^2+4}}.2x + \sqrt[2]{x^2+4}.\left(\frac{x}{2}+\frac{1}{2} \right) \left(\frac{x^2+2x}{4} \right).\frac{1}{\sqrt[2]{x^2+4}}.2x + \sqrt[2]{x^2+4}.\left(\frac{x}{2}+\frac{1}{2} \right)](/latexrender/pictures/caf5488f14f2d3fd0b1d74cf46421c50.png)
![2ln(x+\sqrt[2]{x^2+4}) 2ln(x+\sqrt[2]{x^2+4})](/latexrender/pictures/04f50ce3e2cbe5df95ef9b1bb80f8f7a.png) temos que derivar isso daí..
temos que derivar isso daí..![(x+\sqrt[2]{x^2+4}) (x+\sqrt[2]{x^2+4})](/latexrender/pictures/5032e5aa1fd4b22994ef36cf5825ae82.png) :
:![2.\frac{1}{(x+\sqrt[2]{x^2+4})}.\frac{d}{dx}(x)+\sqrt[2]{x^2+4}) 2.\frac{1}{(x+\sqrt[2]{x^2+4})}.\frac{d}{dx}(x)+\sqrt[2]{x^2+4})](/latexrender/pictures/887de4766c2517843ea8090ff2ef4ae8.png) ( observe que você tem uma soma, então deve derivar um e outro:
( observe que você tem uma soma, então deve derivar um e outro: ![\frac{d}{dx}(x)+\frac{d}{dx}\sqrt[2]{x^2+4} \frac{d}{dx}(x)+\frac{d}{dx}\sqrt[2]{x^2+4}](/latexrender/pictures/3bd8b63c26a3b2ca933e51bb9f18bebb.png) . só que neste ultimo trecho, você cai em outra regra da cadeia:
. só que neste ultimo trecho, você cai em outra regra da cadeia:![\left(\frac{x^2+2x}{4} \right).\frac{1}{\sqrt[2]{x^2+4}}.2x + \sqrt[2]{x^2+4}.\left(\frac{x}{2}+\frac{1}{2} \right)- 2.\frac{1}{(x+\sqrt[2]{x^2+4})}.\frac{d}{dx}(x)+\sqrt[2]{x^2+4}) \left(\frac{x^2+2x}{4} \right).\frac{1}{\sqrt[2]{x^2+4}}.2x + \sqrt[2]{x^2+4}.\left(\frac{x}{2}+\frac{1}{2} \right)- 2.\frac{1}{(x+\sqrt[2]{x^2+4})}.\frac{d}{dx}(x)+\sqrt[2]{x^2+4})](/latexrender/pictures/bff0c84c74856930c4bfe7465ecc39b3.png)