 por beel » Ter Out 04, 2011 22:58
por beel » Ter Out 04, 2011 22:58
Derivada de f(x)=x².tg²(x²)
= (x²)'.tg²(x²) + x²(tg²(x²))'
= 2x.tg²(x²) + x².2tg(x²).sec²(x²)
é isso?
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Neperiano » Qua Out 05, 2011 15:09
por Neperiano » Qua Out 05, 2011 15:09
Ola
Não seria x^2.2xtg...
Porque o u é x^2 e sua derivada é 2x
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por beel » Sex Out 07, 2011 20:49
por beel » Sex Out 07, 2011 20:49
Nao entendi essa ultima derivação...
a derivada de tg²(x²) nao seria apenas
2xtg(x²).tg(x²)' = 2xtg(x²).sec²(x²) ?
na duvida de outro exercicio que postei aqui fiz o contrario, tentei derivar a mais do que deveria,
e nesse, tentei derivar menos....

-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Sáb Out 08, 2011 18:20
por LuizAquino » Sáb Out 08, 2011 18:20
isanobile escreveu:Nao entendi essa ultima derivação...
a derivada de tg²(x²) nao seria apenas
2xtg(x²).tg(x²)' = 2xtg(x²).sec²(x²) ?
Não!Note que você pode escrever as seguintes funções:
(i)

(ii)

(iii)
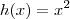
Fazendo a composição dessas funções, note que

.
Portanto, para calcular
![\left[\textrm{tg}\,^2\left(x^2\right)\right]^\prime \left[\textrm{tg}\,^2\left(x^2\right)\right]^\prime](/latexrender/pictures/608c253a322e0d8614a715324200e23d.png)
precisamos calcular
![[f(g(h(x)))]^\prime [f(g(h(x)))]^\prime](/latexrender/pictures/4024a00abf95d2b60750b16a2dccfcd3.png)
.
Aplicando a regra da cadeia, temos que:
![[f(g(h(x)))]^\prime = f^\prime(g(h(x)))[g(h(x))]^\prime = f^\prime(g(h(x)))g^\prime(h(x))h^\prime(x) [f(g(h(x)))]^\prime = f^\prime(g(h(x)))[g(h(x))]^\prime = f^\prime(g(h(x)))g^\prime(h(x))h^\prime(x)](/latexrender/pictures/45eabb74d69d64bb30548e1bc29ccac2.png)
Agora faça as substituições e você deve obter
![\left[\textrm{tg}\,^2\left(x^2\right)\right]^\prime = 4x\,\textrm{tg}\,\left(x^2\right) \sec^2 \left(x^2\right) \left[\textrm{tg}\,^2\left(x^2\right)\right]^\prime = 4x\,\textrm{tg}\,\left(x^2\right) \sec^2 \left(x^2\right)](/latexrender/pictures/2312bd0e6b1ff5ddc32c205fddd2cca6.png)
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por beel » Qui Out 13, 2011 12:33
por beel » Qui Out 13, 2011 12:33
Ok, obrigada.
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [CALCULO] derivada de função composta
por beel » Ter Out 04, 2011 22:45
- 4 Respostas
- 2229 Exibições
- Última mensagem por beel

Dom Out 16, 2011 16:55
Cálculo: Limites, Derivadas e Integrais
-
- Derivada - função composta
por core » Qua Out 16, 2013 15:54
- 1 Respostas
- 1330 Exibições
- Última mensagem por Taka

Sáb Nov 02, 2013 21:12
Cálculo: Limites, Derivadas e Integrais
-
- Derivada de função composta
por Fernandobertolaccini » Qua Jul 09, 2014 08:37
- 0 Respostas
- 911 Exibições
- Última mensagem por Fernandobertolaccini

Qua Jul 09, 2014 08:37
Cálculo: Limites, Derivadas e Integrais
-
- derivada de função composta.
por nandooliver008 » Dom Set 21, 2014 19:42
- 1 Respostas
- 1226 Exibições
- Última mensagem por Cleyson007

Seg Set 22, 2014 18:04
Cálculo: Limites, Derivadas e Integrais
-
- Problema com a derivada de uma função composta
por DavidUserCalc » Qui Abr 01, 2010 14:44
- 1 Respostas
- 1951 Exibições
- Última mensagem por Molina

Qui Abr 01, 2010 16:56
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




![\left[\textrm{tg}\,^2\left(x^2\right)\right]^\prime \left[\textrm{tg}\,^2\left(x^2\right)\right]^\prime](/latexrender/pictures/608c253a322e0d8614a715324200e23d.png) . Ou seja, temos que:
. Ou seja, temos que:![\left[\,\textrm{tg}\,^2\left(x^2\right)\right]^\prime = 2\,\textrm{tg}\,\left(x^2\right)\left[\textrm{tg}\,\left(x^2\right)\right]^\prime \left[\,\textrm{tg}\,^2\left(x^2\right)\right]^\prime = 2\,\textrm{tg}\,\left(x^2\right)\left[\textrm{tg}\,\left(x^2\right)\right]^\prime](/latexrender/pictures/5d46c64237f99447fa0db09c4f55288a.png)
![= 2\,\textrm{tg}\,\left(x^2\right) \sec^2 \left(x^2\right)\left[x^2\right]^\prime = 2\,\textrm{tg}\,\left(x^2\right) \sec^2 \left(x^2\right)\left[x^2\right]^\prime](/latexrender/pictures/2b2ca409296124ca2e158ffb50cbd88b.png)






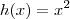
 .
.![\left[\textrm{tg}\,^2\left(x^2\right)\right]^\prime \left[\textrm{tg}\,^2\left(x^2\right)\right]^\prime](/latexrender/pictures/608c253a322e0d8614a715324200e23d.png) precisamos calcular
precisamos calcular ![[f(g(h(x)))]^\prime [f(g(h(x)))]^\prime](/latexrender/pictures/4024a00abf95d2b60750b16a2dccfcd3.png) .
.![[f(g(h(x)))]^\prime = f^\prime(g(h(x)))[g(h(x))]^\prime = f^\prime(g(h(x)))g^\prime(h(x))h^\prime(x) [f(g(h(x)))]^\prime = f^\prime(g(h(x)))[g(h(x))]^\prime = f^\prime(g(h(x)))g^\prime(h(x))h^\prime(x)](/latexrender/pictures/45eabb74d69d64bb30548e1bc29ccac2.png)
![\left[\textrm{tg}\,^2\left(x^2\right)\right]^\prime = 4x\,\textrm{tg}\,\left(x^2\right) \sec^2 \left(x^2\right) \left[\textrm{tg}\,^2\left(x^2\right)\right]^\prime = 4x\,\textrm{tg}\,\left(x^2\right) \sec^2 \left(x^2\right)](/latexrender/pictures/2312bd0e6b1ff5ddc32c205fddd2cca6.png) .
.

