por Phisic » Sáb Out 01, 2011 15:38
http://pt.wikipedia.org/wiki/Matriz_de_rota%C3%A7%C3%A3oOla, estou com dificuldade em implementar uma rotação num ponto do r3 como ensina o link acima.
Tendo um ponto qualquer no r3, gostaria de aplicar um rotação de 10º em sua origem, minha dúvida é como realizar a tarefa,
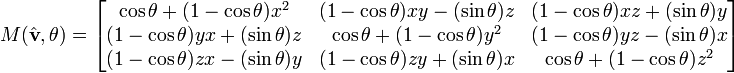, ajudaria se alguem puder fazer uma demostração de como fazer isso.
-
Phisic
- Novo Usuário
-
- Mensagens: 9
- Registrado em: Qui Jul 21, 2011 12:32
- Localização: Cascavel Pr.
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: formado
por LuizAquino » Ter Out 04, 2011 21:00
Veja se a apresentação abaixo pode lhe ajudar.
Título: "Computação Gráfica - Geometria de Transformações - Parte II: Coordenadas e Transformações Homogêneas"
Autor: Luiz M. G. Gonçalves
Arquivo: "transformacao2.ppt"
Página:
15462 Noteshttp://www.dca.ufrn.br/~lmarcos/courses ... index.html
-
LuizAquino
- Colaborador Moderador - Professor
-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ponto da reta r que é eqüidistante do ponto A e do ponto B
por gutorocher » Qua Jul 21, 2010 14:01
- 12 Respostas
- 14825 Exibições
- Última mensagem por gutorocher
Sex Jul 23, 2010 13:04
Geometria Analítica
-
- [Vetores] Ponto de reta próximo a outros pares de ponto
por cmcrz97 » Ter Jun 19, 2018 20:29
- 0 Respostas
- 2806 Exibições
- Última mensagem por cmcrz97
Ter Jun 19, 2018 20:29
Álgebra Linear
-
- [Ponto Crítico e Ponto de Inflexão e intervalos] Dúvidas em
por Andre Lopes » Qua Set 26, 2012 00:37
- 2 Respostas
- 3233 Exibições
- Última mensagem por MarceloFantini
Qui Set 27, 2012 06:56
Cálculo: Limites, Derivadas e Integrais
-
- [ponto critico]duvida sobre achar o ponto critico
por nayra suelen » Dom Mai 27, 2012 19:38
- 2 Respostas
- 2310 Exibições
- Última mensagem por nayra suelen
Qua Mai 30, 2012 13:23
Cálculo: Limites, Derivadas e Integrais
-
- Ângulos
por admin » Sex Set 07, 2007 06:42
- 3 Respostas
- 12771 Exibições
- Última mensagem por Numwantida
Qui Mai 24, 2018 05:06
Pérolas
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30
Então, o exercicio pede para encontrar
.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:
Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):
Somando a primeira e a segunda equação:
Finalmente:
Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
