olá
boa noite
não consigo resolver essas integrais:
?dx/(e^x+e^-x)
?sen(3x)dx/(³?(cos3x)^4)
?dx/(?x*(?x+1))
?ln(x)^3dx/(x)
?x²cos²(x)dx
parece ser trabalhoso, mas por favor quem souber responda a este topico.



vinicius cruz escreveu:
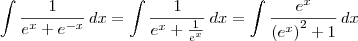
 e
e 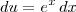 .
.vinicius cruz escreveu:
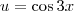 e
e 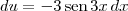 .
.vinicius cruz escreveu:
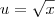 e
e 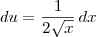 .
.vinicius cruz escreveu:
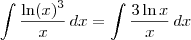
 e
e 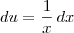 .
.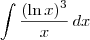 ,
,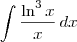 .
. e
e 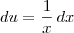 .
.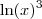 , é tal que
, é tal que 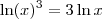 . Já a expressão (ln(x))^3, que pode ser escrita como
. Já a expressão (ln(x))^3, que pode ser escrita como 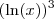 , é tal que
, é tal que 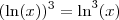 .
.vinicius cruz escreveu:
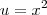 e
e 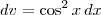 .
.

vinicius cruz escreveu:mas na primeira questão eu não entendi como o "e^x" foi parar em cima ??
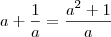 .
.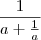 .
.vinicius cruz escreveu:e na segunda questão quais os passos seguintes, pois eu parei em:
2??x/[u*(?x+1)]
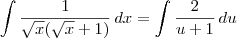


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

