 por andersontricordiano » Seg Set 26, 2011 17:51
por andersontricordiano » Seg Set 26, 2011 17:51
Resolva, em R, as seguintes equações:
a)
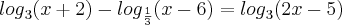
b)
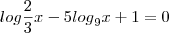
c)

As respostas são:
a)S={7}
b)S={
![{9,\sqrt[]{2}} {9,\sqrt[]{2}}](/latexrender/pictures/847bedae4d9cf81f64ffd7ddf021aa7d.png)
}
c)S={
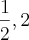
}
Agradeço muito quem resolver esse calculo!
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Seg Set 26, 2011 20:59
por MarceloFantini » Seg Set 26, 2011 20:59
Na primeira, aplique a propriedade que
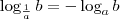
e também
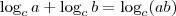
, lembrando das condições de existência.
No segundo não consigo entender a expressão.
No terceiro, use a propriedade
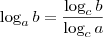
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por DanielFerreira » Dom Jan 08, 2012 16:52
por DanielFerreira » Dom Jan 08, 2012 16:52
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Dom Jan 08, 2012 17:21
por DanielFerreira » Dom Jan 08, 2012 17:21
andersontricordiano escreveu:Resolva, em R, as seguintes equações:
c)

As respostas são:
c)S={
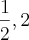
}
Passemos p/ a base 2:
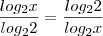
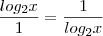

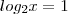
e
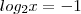

e


e

"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Resolva em C, as seguintes equações:
por andersontricordiano » Dom Jan 15, 2012 17:27
- 3 Respostas
- 3100 Exibições
- Última mensagem por fraol

Dom Jan 15, 2012 20:12
Números Complexos
-
- Resolva as seguintes equações:
por andersontricordiano » Seg Jan 23, 2012 12:51
- 2 Respostas
- 1640 Exibições
- Última mensagem por Arkanus Darondra

Seg Jan 23, 2012 13:07
Estatística
-
- Resolva as seguintes equações:
por andersontricordiano » Qui Jan 26, 2012 14:48
- 2 Respostas
- 1976 Exibições
- Última mensagem por Molina

Qui Jan 26, 2012 15:31
Estatística
-
- (probabilidade) Resolva as seguintes equações
por andersontricordiano » Sex Fev 10, 2012 12:51
- 3 Respostas
- 2003 Exibições
- Última mensagem por MarceloFantini

Sáb Fev 11, 2012 14:44
Estatística
-
- Classifique e resolva , os seguintes sistemas homogêneos.
por andersontricordiano » Ter Jan 03, 2012 23:38
- 1 Respostas
- 3240 Exibições
- Última mensagem por Arkanus Darondra

Qui Jan 05, 2012 00:23
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
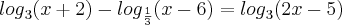
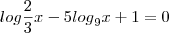

![{9,\sqrt[]{2}} {9,\sqrt[]{2}}](/latexrender/pictures/847bedae4d9cf81f64ffd7ddf021aa7d.png) }
}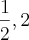 }
}
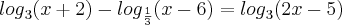
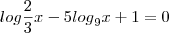

![{9,\sqrt[]{2}} {9,\sqrt[]{2}}](/latexrender/pictures/847bedae4d9cf81f64ffd7ddf021aa7d.png) }
}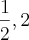 }
}
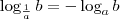 e também
e também 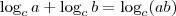 , lembrando das condições de existência.
, lembrando das condições de existência.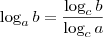 .
.

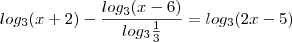


![log_{3} [(x + 2)(x - 6)] = log_{3} (2x - 5) log_{3} [(x + 2)(x - 6)] = log_{3} (2x - 5)](/latexrender/pictures/06e5ff14bd76efe4c3b96b93be199bbd.png)
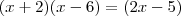

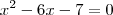
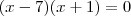
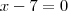


}
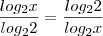
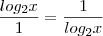

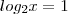 e
e 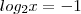
 e
e 
 e
e 

