 por Faby » Seg Set 19, 2011 10:55
por Faby » Seg Set 19, 2011 10:55
Calcule a área:
O conjunto A delimitado pelos gráficos de

e

para
![x \in \left[0,2\pi \right] x \in \left[0,2\pi \right]](/latexrender/pictures/9521c4494f24fde7214e36e94c190d0d.png)
.
Resolução:
Já fiz o gráfico,
a fórmula a ser utilizada seria
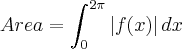
??
Editado pela última vez por
Faby em Seg Set 19, 2011 11:08, em um total de 1 vez.
-
Faby
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 10:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Seg Set 19, 2011 10:58
por LuizAquino » Seg Set 19, 2011 10:58
Faby,
Por favor, poste também suas tentativas e dúvidas.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Faby » Ter Set 20, 2011 12:56
por Faby » Ter Set 20, 2011 12:56
Pensei no seguinte:
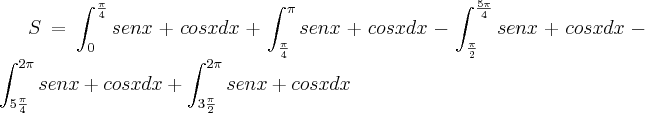
Isso tudo seria
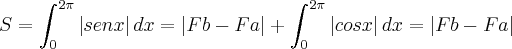
???
-
Faby
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 10:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Faby » Qua Set 21, 2011 01:52
por Faby » Qua Set 21, 2011 01:52
...estava errando pq não tinha compreendido como "montar' a integral. Com o seu desenho o raciocínio foi mais fácil, obrigada
Calculei as integrais separadamente, e cheguei ao seguinte resultado
=(?2-2)+(?2-2)+1+|-1|+|-?2+2|+|-1|+|-1|+|1|=
=?2+1 u.a.
será que acertei?? ou devo calcular novamente...
-
Faby
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 10:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Qua Set 21, 2011 11:51
por LuizAquino » Qua Set 21, 2011 11:51
Faby escreveu:será que acertei?? ou devo calcular novamente...
Você ainda não acertou. Calcule novamente.
Por exemplo, note que:
![\int_0^{\frac{\pi}{4}} \cos x - \,\textrm{sen}\, x \, dx = \left[\textrm{sen}\,x + \cos x\right]_0^{\frac{\pi}{4}} \int_0^{\frac{\pi}{4}} \cos x - \,\textrm{sen}\, x \, dx = \left[\textrm{sen}\,x + \cos x\right]_0^{\frac{\pi}{4}}](/latexrender/pictures/cda743f98183d57e615c13ad7388868f.png)
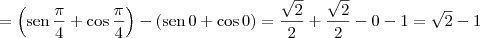
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Faby » Qua Set 21, 2011 15:47
por Faby » Qua Set 21, 2011 15:47
calculando novamente, cheguei ao seguinte resultado:
![(\sqrt[]{2}-1)+(\sqrt[]{2}-1)+ \left|-1 \right|+\left|-\sqrt[]{2}+1 \right|+\left|-\sqrt[]{2} +1\right|+\left|-1 \right|+1=4 \sqrt[]{2}-1 (\sqrt[]{2}-1)+(\sqrt[]{2}-1)+ \left|-1 \right|+\left|-\sqrt[]{2}+1 \right|+\left|-\sqrt[]{2} +1\right|+\left|-1 \right|+1=4 \sqrt[]{2}-1](/latexrender/pictures/b3f0e2a3191ce7f4cabc9cffc3f41b85.png)
E agora??
obrigada
-
Faby
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 10:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Faby » Qua Set 21, 2011 16:59
por Faby » Qua Set 21, 2011 16:59
calculei, mas esqueci na hora de digitar
![(\sqrt[]{2}-1)+(\sqrt[]{2}-1)+1+ \left|-1 \right|+\left|-\sqrt[]{2}+1 \right|+\left|-\sqrt[]{2} +1\right|+\left|-1 \right|+1=4 \sqrt[]{2} (\sqrt[]{2}-1)+(\sqrt[]{2}-1)+1+ \left|-1 \right|+\left|-\sqrt[]{2}+1 \right|+\left|-\sqrt[]{2} +1\right|+\left|-1 \right|+1=4 \sqrt[]{2}](/latexrender/pictures/bb6f49300a906e041b7fa8e4aea901c3.png)
acertei??
-
Faby
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 10:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Qua Set 21, 2011 17:10
por LuizAquino » Qua Set 21, 2011 17:10
Faby escreveu:calculei, mas esqueci na hora de digitar
![(\sqrt[]{2}-1)+(\sqrt[]{2}-1)+1+ \left|-1 \right|+\left|-\sqrt[]{2}+1 \right|+\left|-\sqrt[]{2} +1\right|+\left|-1 \right|+1=4 \sqrt[]{2} (\sqrt[]{2}-1)+(\sqrt[]{2}-1)+1+ \left|-1 \right|+\left|-\sqrt[]{2}+1 \right|+\left|-\sqrt[]{2} +1\right|+\left|-1 \right|+1=4 \sqrt[]{2}](/latexrender/pictures/f2e50803799a827499473cbd761add84.png)
acertei??
Agora sim!

Aproveito ainda para indicar outra solução.
Analisando a simetria da figura, note que a área desejada também poderia ter sido calculada por:
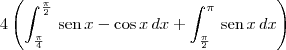
Tente enxergar o porque disso analisando a figura.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Faby » Qua Set 21, 2011 17:37
por Faby » Qua Set 21, 2011 17:37
...pq cada uma das integrais repetem 4 vezes...
nossa, com esta fórmula fica bem mais simplificada.
São muitas contas daquele jeito que fizemos, aí fica fácil de cometer erros.
Muito obrigada pela ajuda matemática!
Estou calculando a outra questão que eu postei.
teria como eu enviar arquivo do word, meu ombro tá reclamando, ou por imagem?
Até +
bjs
-
Faby
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 10:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Qua Set 21, 2011 18:03
por LuizAquino » Qua Set 21, 2011 18:03
Faby escreveu:Estou calculando a outra questão que eu postei.
teria como eu enviar arquivo do word, meu ombro tá reclamando, ou por imagem?
Não é recomendado que você poste a solução dessa forma (através de arquivo). Pois isso prejudica os sistemas de busca.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Cálculo de áreas por integrais
 por Faby » Seg Set 19, 2011 10:50
por Faby » Seg Set 19, 2011 10:50
- 9 Respostas
- 6326 Exibições
- Última mensagem por Faby

Qui Set 22, 2011 00:41
Cálculo: Limites, Derivadas e Integrais
-
- Integrais (áreas) [dúvida]
por citadp » Qua Jun 20, 2012 11:21
- 4 Respostas
- 3187 Exibições
- Última mensagem por Russman

Qui Jun 21, 2012 10:58
Cálculo: Limites, Derivadas e Integrais
-
- Calculo de Áreas utilizando integrais
por Rambox » Ter Jun 14, 2011 14:38
- 2 Respostas
- 2209 Exibições
- Última mensagem por Rambox

Ter Jun 14, 2011 14:54
Cálculo: Limites, Derivadas e Integrais
-
- Interseção entre áreas (Integrais)
 por thejotta » Seg Abr 30, 2018 16:52
por thejotta » Seg Abr 30, 2018 16:52
- 3 Respostas
- 11211 Exibições
- Última mensagem por Gebe

Ter Mai 01, 2018 22:51
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por pseytow » Qui Nov 27, 2008 21:54
- 1 Respostas
- 2810 Exibições
- Última mensagem por Adriano Tavares

Qui Mar 10, 2011 01:52
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e  para
para ![x \in \left[0,2\pi \right] x \in \left[0,2\pi \right]](/latexrender/pictures/9521c4494f24fde7214e36e94c190d0d.png) .
.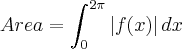

 e
e  para
para ![x \in \left[0,2\pi \right] x \in \left[0,2\pi \right]](/latexrender/pictures/9521c4494f24fde7214e36e94c190d0d.png) .
.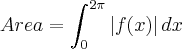


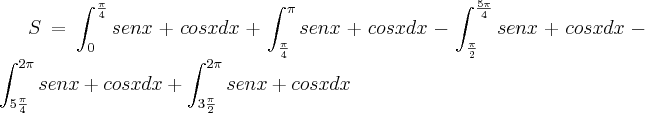
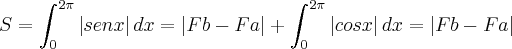

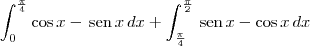
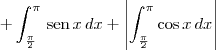
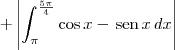




![\int_0^{\frac{\pi}{4}} \cos x - \,\textrm{sen}\, x \, dx = \left[\textrm{sen}\,x + \cos x\right]_0^{\frac{\pi}{4}} \int_0^{\frac{\pi}{4}} \cos x - \,\textrm{sen}\, x \, dx = \left[\textrm{sen}\,x + \cos x\right]_0^{\frac{\pi}{4}}](/latexrender/pictures/cda743f98183d57e615c13ad7388868f.png)
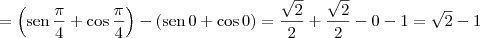

![(\sqrt[]{2}-1)+(\sqrt[]{2}-1)+ \left|-1 \right|+\left|-\sqrt[]{2}+1 \right|+\left|-\sqrt[]{2} +1\right|+\left|-1 \right|+1=4 \sqrt[]{2}-1 (\sqrt[]{2}-1)+(\sqrt[]{2}-1)+ \left|-1 \right|+\left|-\sqrt[]{2}+1 \right|+\left|-\sqrt[]{2} +1\right|+\left|-1 \right|+1=4 \sqrt[]{2}-1](/latexrender/pictures/b3f0e2a3191ce7f4cabc9cffc3f41b85.png)



![(\sqrt[]{2}-1)+(\sqrt[]{2}-1)+1+ \left|-1 \right|+\left|-\sqrt[]{2}+1 \right|+\left|-\sqrt[]{2} +1\right|+\left|-1 \right|+1=4 \sqrt[]{2} (\sqrt[]{2}-1)+(\sqrt[]{2}-1)+1+ \left|-1 \right|+\left|-\sqrt[]{2}+1 \right|+\left|-\sqrt[]{2} +1\right|+\left|-1 \right|+1=4 \sqrt[]{2}](/latexrender/pictures/bb6f49300a906e041b7fa8e4aea901c3.png)


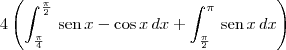



![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.