(EEM-SP) Seja
 a função tal que
a função tal que  . Seja
. Seja 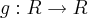 a função tal que
a função tal que 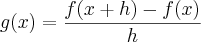 . Calcule g(x).
. Calcule g(x).A resposta que o livro dá é: g(x)=2x+h
Tentei várias vezes, daí tive a idéia de por em evidência o f(x+h), ficou da seguinte forma:
 , isso já considerando f(x) substituído por
, isso já considerando f(x) substituído por 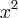 .
.Daí fiz a seguinte relação:
Se f(x)=
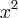 ; e,
; e, ; então,
; então, .
.Aí vem o problema, ao prosseguir o cálculo daí, chego na seguinte situação:

prosseguindo eu chego em:
 ;, logo
;, logo , finalizando em:
, finalizando em: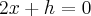 em vez de
em vez de 
Gostaria que me ajudassem a resolver esse problema.
Grato.
Diego


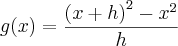
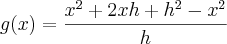

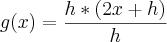
 é a derivada de
é a derivada de 


 .
.



