 por Tito » Dom Ago 21, 2011 05:30
por Tito » Dom Ago 21, 2011 05:30
Olá pessoal...
Este problema me parece bem simples mas não consigo resolve-lo. Tentei da seguinte forma conforme o enunciado.
(BB) Se aplicarmos determinada quantia durante 8 meses, seu montante será de $ 63.000. Caso a aplicação durasse 13 meses, o montante seria de $ 74.250. Qual a taxa mensal empregada...
Eu fiz os seguintes cálculos colocando o montante de 63.000 como capital.
C: 63.000
M: 74.250
J: 74.250 - 63.000 = 11.250
T: 13 - 8 = 5 meses
J=P%C
11.250=P%63.000
P%=0,1786 = 17,86%
P%=i x t
17,86=i x 5
i=3,572
A resposta correta é 5%.
Obrigado.
-
Tito
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Ago 21, 2011 05:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Farmacêutico
- Andamento: formado
 por Caradoc » Dom Ago 21, 2011 11:16
por Caradoc » Dom Ago 21, 2011 11:16
Você pode fazer um sistema:
O montante é o capital + juros
E os juros são o capital * taxa * tempo
Então:


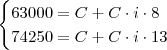
Com duas equações e duas incógnitas você consegue resolver o sistema.
-
Caradoc
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qui Dez 16, 2010 17:17
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Tito » Ter Ago 23, 2011 01:52
por Tito » Ter Ago 23, 2011 01:52
Obrigado Caradoc, demorei mas consegui resolver pelo seu sistema..
Eu peguei a primeira sentença e negativei: -63.000 = -C -Ci8
depois fiz adição de sistemas com: 74.250 = C + Ci13
isolei o "C": C = 2250/i
e substitui na primeira sentença do sistema.
encontrei 0,05 = 5%
-
Tito
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Ago 21, 2011 05:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Farmacêutico
- Andamento: formado
 por LuizAquino » Ter Ago 23, 2011 09:47
por LuizAquino » Ter Ago 23, 2011 09:47
Tito escreveu:Eu peguei a primeira sentença e negativei: -63.000 = -C -Ci8
depois fiz adição de sistemas com: 74.250 = C + Ci13
isolei o "C": C = 2250/i
e substitui na primeira sentença do sistema.
encontrei 0,05 = 5%
Nesse caso bastava dividir membro a membro a primeira equação pela segunda. Isto é, resolver a equação:

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida em montante e taxa de juros.
por Marcosaf » Seg Set 15, 2014 14:41
- 3 Respostas
- 3978 Exibições
- Última mensagem por jcmatematica

Ter Set 16, 2014 16:50
Matemática Financeira
-
- [Montante captalizado] Encontrar montante captalizado
por donizeth » Sex Jun 07, 2013 09:03
- 0 Respostas
- 1398 Exibições
- Última mensagem por donizeth

Sex Jun 07, 2013 09:03
Matemática Financeira
-
- Juro Composto - Encontrar taxa
por zero_br » Qui Dez 06, 2012 18:04
- 0 Respostas
- 2038 Exibições
- Última mensagem por zero_br

Qui Dez 06, 2012 18:04
Matemática Financeira
-
- Juros, Encontrar Taxa Mensal
por elisamaria » Seg Mar 09, 2015 16:20
- 0 Respostas
- 2409 Exibições
- Última mensagem por elisamaria

Seg Mar 09, 2015 16:20
Matemática Financeira
-
- Encontrar a taxa efetiva anual da operação
 por cristianetimmbonow » Seg Mar 20, 2017 10:54
por cristianetimmbonow » Seg Mar 20, 2017 10:54
- 0 Respostas
- 4678 Exibições
- Última mensagem por cristianetimmbonow

Seg Mar 20, 2017 10:54
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




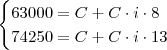



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.