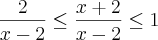
A resposta do livro é:
![\left(-\infty;0 \right] \left(-\infty;0 \right]](/latexrender/pictures/d2db8b4f54518928b27a17cc0f5fd375.png)
Meu resultado dá sempre VAZIO. As incógnitas se cancelam.
E agora?

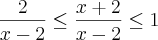
![\left(-\infty;0 \right] \left(-\infty;0 \right]](/latexrender/pictures/d2db8b4f54518928b27a17cc0f5fd375.png)


renanrdaros escreveu:
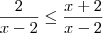 ;
;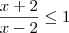 .
.


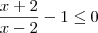
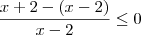


LuizAquino escreveu:
 . Então não existe solução para
. Então não existe solução para 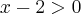 .
.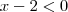 :
:
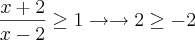
 ???
???
renanrdaros escreveu:
Resulta em. Então não existe solução para
.
renanrdaros escreveu:

LuizAquino escreveu:De novo você cometeu o erro de "passar" o (x- 2) multiplicando!

renanrdaros escreveu:Eu NUNCA multipliquei em cruz. Eu apenas multiplico ambos os lados por (x - 2). O que é completamente correto, desde que se considere dois casos distintos: um em que (x - 2) é menor que zero e outro em que (x - 2) é maior que zero.
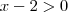
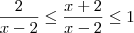 por
por  ficamos com:
ficamos com: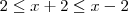
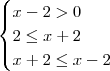
 .
.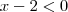
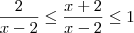 por
por  ficamos com:
ficamos com: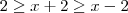

![S_2 = (-\infty,\, 0] S_2 = (-\infty,\, 0]](/latexrender/pictures/05bfd2c014549f7c7e724836520595e8.png) .
.![S = S_1 \cup S_2 = (-\infty,\, 0] S = S_1 \cup S_2 = (-\infty,\, 0]](/latexrender/pictures/90661b4286ef834d8d1846c336d758cf.png) .
.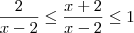 obtemos o sistema:
obtemos o sistema: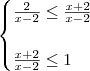

![S_1 = (-\infty,\, 0] \cup (2,\,+\infty) S_1 = (-\infty,\, 0] \cup (2,\,+\infty)](/latexrender/pictures/56e946f8b7e9df2efab7a7f0a3d2ca61.png) .
.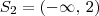 .
.![S = S_1 \cap S_2 = (-\infty,\, 0] S = S_1 \cap S_2 = (-\infty,\, 0]](/latexrender/pictures/ff453dc67dd258eb2dd3e0f30536ac6c.png) .
.

renanrdaros escreveu:Ou eu estou muito enganado, ou a sua primeira solução é a mesma coisa que eu fiz e que você tinha falado que eu estava fazendo errado.
renanrdaros escreveu:É isso? Apenas desconsidero a segunda inequação e fico com???


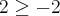 . É isso?
. É isso?
renanrdaros escreveu:A minha dúvida era esta mesmo: O que fazer com a última inequação do sistema?
Ela me diz apenas que. É isso?
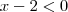 (cuja a solução é
(cuja a solução é  ) e obteve:
) e obteve:
![S_2 = (-\infty,\, 0] S_2 = (-\infty,\, 0]](/latexrender/pictures/05bfd2c014549f7c7e724836520595e8.png) .
. 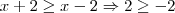
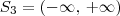 (pois para qualquer valor real x temos que
(pois para qualquer valor real x temos que  ).
).![S = S_1 \cap S_2 \cap S_3 = (-\infty,\, 0] S = S_1 \cap S_2 \cap S_3 = (-\infty,\, 0]](/latexrender/pictures/e8721029b5802d88d4b7d6158e1ff33f.png) .
.
renanrdaros escreveu:
Ou seja, a solução dessa inequação é S_3 =(pois para qualquer valor real x temos que
)

Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes