 por Claudin » Qui Ago 04, 2011 03:00
por Claudin » Qui Ago 04, 2011 03:00
Não consigo encontrar uma maneira fácil de encontrar raízes, na fatoração de polinômios do 4º grau, ou até do 5º grau. Alguém tem alguma dica específica que facilite os exercícios.
Deduzindo algumas raízes e utilizando o
WolframAlpha, gostaria de saber se tem algumas dicas para fatoração de polinômios de 4º,5º,6º...graus.
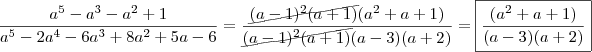
A resolução está correta?
Editado pela última vez por
Claudin em Qui Ago 04, 2011 15:47, em um total de 1 vez.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por giulioaltoe » Qui Ago 04, 2011 15:45
por giulioaltoe » Qui Ago 04, 2011 15:45
porque voce desconsiderou o (a+2) do denominador na penultima conta?
-
giulioaltoe
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Jun 23, 2011 21:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia metalurgica e mat - UENF
- Andamento: cursando
 por Claudin » Qui Ago 04, 2011 15:47
por Claudin » Qui Ago 04, 2011 15:47
Foi falta de atenção mesmo.

"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por giulioaltoe » Qui Ago 04, 2011 15:57
por giulioaltoe » Qui Ago 04, 2011 15:57
tem algumas respostas que vao ficar meio grandes mesmo, portanto nao se assuste se seu resultado final nao estiver muito enxuto!
-
giulioaltoe
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Jun 23, 2011 21:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia metalurgica e mat - UENF
- Andamento: cursando
 por Claudin » Qui Ago 04, 2011 15:59
por Claudin » Qui Ago 04, 2011 15:59
Com certeza.

"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [fatoração] fatoração de polinômio do quarto grau.
por +Danilo2 » Qui Set 29, 2016 10:43
- 5 Respostas
- 8909 Exibições
- Última mensagem por +Danilo2

Sáb Out 08, 2016 18:17
Polinômios
-
- fatoração de Polinômio fatoração de agrupamento
por Estudante13 » Sex Nov 09, 2012 22:52
- 1 Respostas
- 3255 Exibições
- Última mensagem por Cleyson007

Sex Nov 09, 2012 23:06
Álgebra Elementar
-
- [fatoração] Exercício de Fatoração
por Cleyson007 » Qua Abr 30, 2008 00:39
- 3 Respostas
- 8820 Exibições
- Última mensagem por admin

Qua Abr 30, 2008 02:15
Álgebra Elementar
-
- Fatoração
por Rogerioeetc » Sex Jul 24, 2009 02:00
- 2 Respostas
- 2536 Exibições
- Última mensagem por Rogerioeetc

Dom Jul 26, 2009 14:26
Álgebra Elementar
-
- Fatoração
por Jaqueline Pimenta » Qui Out 01, 2009 11:50
- 5 Respostas
- 4075 Exibições
- Última mensagem por Jaqueline Pimenta

Seg Out 05, 2009 12:05
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
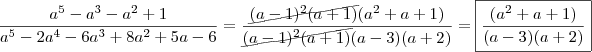

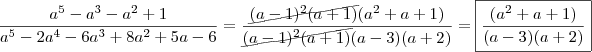







 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
