 por Maykids » Sáb Jul 09, 2011 01:19
por Maykids » Sáb Jul 09, 2011 01:19
então dando mais uma olhada aqui para a avaliação final:
me deparei com esses 2 exercicios:
1-Para a função f definida por :
![f(x) = -\sqrt[]{(2-x)} f(x) = -\sqrt[]{(2-x)}](/latexrender/pictures/609f02706532d2499b0b586ce9bf93d0.png)
, x<1

se
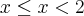
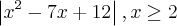
faço F(1) aplico os limites laterais, só que eu erro ai, pois eu acho a+b e depois nao sei como sabe o valor de cada,
2- verificar se uma Função é continua em toda reta R:
ex:

att,
Maycon
-
Maykids
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Dom Mar 20, 2011 12:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de computação
- Andamento: cursando
 por LuizAquino » Ter Jul 12, 2011 11:36
por LuizAquino » Ter Jul 12, 2011 11:36
O texto do exercício 1 não está completo. Ele deve ser algo como:
Determine as constantes a e b para que a função f definida por
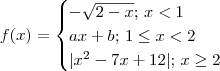
seja contínua em todo

.
Nesse caso, você irá determinar as constantes ao notar que f deve ser tal que:
(i)
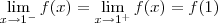
(ii)
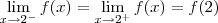
Já no exercício 2, note que a função não está definida em x = -2.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral Descobrindo valores.
por Maykids » Qua Jun 29, 2011 12:33
- 1 Respostas
- 1642 Exibições
- Última mensagem por LuizAquino

Qua Jun 29, 2011 16:22
Cálculo: Limites, Derivadas e Integrais
-
- Quais os possíveis valores que satisfazem os valores reais
por andersontricordiano » Seg Fev 24, 2014 22:53
- 1 Respostas
- 5157 Exibições
- Última mensagem por Russman

Ter Fev 25, 2014 02:17
Números Complexos
-
- Descobrindo os casais
por Cleyson007 » Dom Fev 07, 2010 14:18
- 1 Respostas
- 1481 Exibições
- Última mensagem por Elcioschin

Seg Fev 08, 2010 22:37
Desafios Médios
-
- DESCOBRINDO OS DIVISORES DA TAXA i%
por leo_30_rj » Sáb Ago 14, 2010 17:17
- 2 Respostas
- 1753 Exibições
- Última mensagem por Douglasm

Seg Ago 16, 2010 13:59
Matemática Financeira
-
- equação de segundo grau( descobrindo as raizes)
por arturmedeiros2010 » Qui Fev 13, 2014 15:34
- 1 Respostas
- 1363 Exibições
- Última mensagem por Russman

Sex Fev 14, 2014 00:15
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f(x) = -\sqrt[]{(2-x)} f(x) = -\sqrt[]{(2-x)}](/latexrender/pictures/609f02706532d2499b0b586ce9bf93d0.png) , x<1
, x<1 se
se 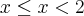
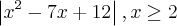



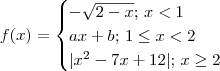 seja contínua em todo
seja contínua em todo  .
.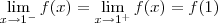
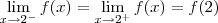

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.