 por giulioaltoe » Qua Jul 06, 2011 00:20
por giulioaltoe » Qua Jul 06, 2011 00:20
a questao e essa
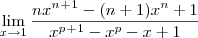
entao fiz o desenvolvimento e cheguei a a algo do tipo
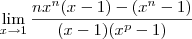
a partir dai nao achei termos em comum para cortar termos e chegar a uma reposta concreta se alguem souber agradeço

eu cheguei a outra fatoração tbm que h
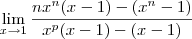
mas nao sai dai!!
Editado pela última vez por
giulioaltoe em Qua Jul 06, 2011 01:00, em um total de 1 vez.
-
giulioaltoe
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Jun 23, 2011 21:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia metalurgica e mat - UENF
- Andamento: cursando
 por LuizAquino » Qua Jul 06, 2011 00:52
por LuizAquino » Qua Jul 06, 2011 00:52
giulioaltoe escreveu:a questao e essa

(...)
Reveja o texto original do exercício, pois o limite deve ser algo como
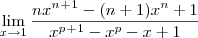
.
giulioaltoe escreveu:fiz o desenvolvimento e cheguei a a algo do tipo

a partir dai nao achei termos em comum para cortar termos e chegar a uma reposta
Dica: use o produto notável descrito na mensagem abaixo para desenvolver

:
viewtopic.php?f=120&t=5302#p18125
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por giulioaltoe » Qua Jul 06, 2011 00:57
por giulioaltoe » Qua Jul 06, 2011 00:57
escrevi errado msm esse delta nao existe, mas se eu tenho uma potencia com radical indefinido como posso saber ate onde devo fazer o produto notavel, existe alguma propriedade que resuma isso!?
-
giulioaltoe
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Jun 23, 2011 21:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia metalurgica e mat - UENF
- Andamento: cursando
 por LuizAquino » Qua Jul 06, 2011 10:31
por LuizAquino » Qua Jul 06, 2011 10:31
giulioaltoe escreveu:eu tenho uma potencia com radical indefinido como posso saber ate onde devo fazer o produto notavel, existe alguma propriedade que resuma isso!?
Assim como foi feito na
mensagem que eu indiquei acima, você usará a reticências para simbolizar o desenvolvimento desse produto notável.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por giulioaltoe » Qua Jul 06, 2011 19:07
por giulioaltoe » Qua Jul 06, 2011 19:07
como

na hora de substituir a equação

a resposta seria (x-1)(n) ja que sao n termos e multiplicando eles por 1 seria n a resposta dessa parte da equação?
-
giulioaltoe
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Jun 23, 2011 21:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia metalurgica e mat - UENF
- Andamento: cursando
 por MarceloFantini » Qua Jul 06, 2011 19:42
por MarceloFantini » Qua Jul 06, 2011 19:42
Giulio, note que
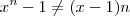
, são bem diferentes. Sobre seu limite, não vejo indeterminação quando

. Você tentou substituir? Tem a resposta?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por giulioaltoe » Qui Jul 07, 2011 15:22
por giulioaltoe » Qui Jul 07, 2011 15:22
eu peguei

ai o produto notavel disso

e substituindo o 1 no lugar de x eu acharei n termos que sao 1 elevado a um valor n que independente dele vai dar um sendo assim terrei

que sera n!
-
giulioaltoe
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Jun 23, 2011 21:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia metalurgica e mat - UENF
- Andamento: cursando
 por giulioaltoe » Qui Jul 07, 2011 15:33
por giulioaltoe » Qui Jul 07, 2011 15:33
mas na questao eu tenho que extrair o

para posteriormente poder cortar com a expressao de baixo, pois se nao o limite fica indeterminado!
-
giulioaltoe
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Jun 23, 2011 21:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia metalurgica e mat - UENF
- Andamento: cursando
 por LuizAquino » Qui Jul 07, 2011 17:37
por LuizAquino » Qui Jul 07, 2011 17:37
Temos que
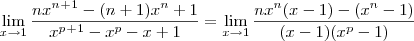
Usando produtos notáveis, sabemos que
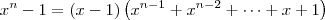
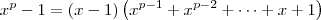
Sendo assim, ficamos com
![\lim_{ x\to1}\frac{nx^n(x-1)-(x^n-1)}{(x-1)(x^p-1)} = \lim_{ x\to1}\frac{(x-1)\left[nx^n - \left(x^{n-1} + x^{n-2} + \cdots + x + 1\right)\right]}{(x-1)(x - 1)\left(x^{p-1} + x^{p-2} + \cdots + x + 1\right)} \lim_{ x\to1}\frac{nx^n(x-1)-(x^n-1)}{(x-1)(x^p-1)} = \lim_{ x\to1}\frac{(x-1)\left[nx^n - \left(x^{n-1} + x^{n-2} + \cdots + x + 1\right)\right]}{(x-1)(x - 1)\left(x^{p-1} + x^{p-2} + \cdots + x + 1\right)}](/latexrender/pictures/6315765ec26517366e19bd4a290eb47c.png)
Mas, temos que
![\lim_{ x\to1}\frac{(x-1)\left[nx^n - \left(x^{n-1} + x^{n-2} + \cdots + x + 1\right)\right]}{(x-1)(x - 1)\left(x^{p-1} + x^{p-2} + \cdots + x + 1\right)} = \lim_{ x\to1}\frac{nx^n - \left(x^{n-1} + x^{n-2} + \cdots + x + 1\right)}{(x - 1)\left(x^{p-1} + x^{p-2} + \cdots + x + 1\right)} \lim_{ x\to1}\frac{(x-1)\left[nx^n - \left(x^{n-1} + x^{n-2} + \cdots + x + 1\right)\right]}{(x-1)(x - 1)\left(x^{p-1} + x^{p-2} + \cdots + x + 1\right)} = \lim_{ x\to1}\frac{nx^n - \left(x^{n-1} + x^{n-2} + \cdots + x + 1\right)}{(x - 1)\left(x^{p-1} + x^{p-2} + \cdots + x + 1\right)}](/latexrender/pictures/72087ff4960c88c45af3d09b3639c776.png)
É fácil perceber no último limite que no denominador temos algo aproximando-se de 0. Mas, no numerador também temos algo aproximando-se de 0, pois temos n parcelas naquela soma e quando x tender a 1 ficaremos com n - n = 0. Em resumo, o último limite é uma indeterminação do tipo 0/0.
Para remover essa indeterminação precisamos dividir o numerador e o denominador por

.
É fácil perceber que a divisão de

por

resulta em

.
Agora, é necessário dividir

por

. Aplicando os conhecimentos sobre divisão de polinômios, obtemos:
![\left[nx^n - \left(x^{n-1} + x^{n-2} + \cdots + x + 1\right)\right] \div (x - 1) \left[nx^n - \left(x^{n-1} + x^{n-2} + \cdots + x + 1\right)\right] \div (x - 1)](/latexrender/pictures/941b7d8ce45174ec7dc2579fd8c2b22e.png)
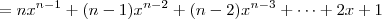
Portanto, temos que

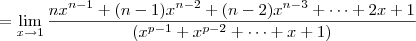
Note que no denominador aparecerá a soma 1 + 1 + ... + 1 + 1, com p parcelas. Isso resulta em p.
Já no numerador irá aparecer a soma n + (n - 1) + (n - 2) + ... + 2 + 1. Ora, isso nada mais é do que a soma dos números inteiros indo de 1 até n, que como sabemos (por p. a.) é dada por
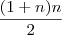
.
Sendo assim, temos que
 Observação
ObservaçãoCaso você não esteja bem treinado na divisão de polinômios, eu recomendo que você faça uma revisão.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por giulioaltoe » Qui Jul 07, 2011 20:50
por giulioaltoe » Qui Jul 07, 2011 20:50
e rapais, sua dica da revisao de divisão de polinomio e uma boa, porque foi a partir dai mesmo qua nao sabia fazer mais nada, mesmo com voce desenvolvendo ai nao lembro nada disso!! muito menos o de p.a muito obrigado vou procurar algo a respeito na intenet!
-
giulioaltoe
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Jun 23, 2011 21:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia metalurgica e mat - UENF
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 5409 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]Preciso de ajuda para calcular alguns limites
por Pessoa Estranha » Ter Jul 16, 2013 17:15
- 2 Respostas
- 4755 Exibições
- Última mensagem por LuizAquino

Qua Jul 17, 2013 09:12
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Ajuda com limites no infinito e continuidade
 por umbrorz » Dom Abr 15, 2012 00:54
por umbrorz » Dom Abr 15, 2012 00:54
- 3 Respostas
- 4782 Exibições
- Última mensagem por umbrorz

Seg Abr 16, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
-
- [limites] exercicio de calculo envolvendo limites
por lucasdemirand » Qua Jul 10, 2013 00:45
- 1 Respostas
- 4808 Exibições
- Última mensagem por e8group

Sáb Jul 20, 2013 13:08
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Dúvida sobre limites laterais
por Subnik » Sáb Abr 04, 2015 18:24
- 1 Respostas
- 2793 Exibições
- Última mensagem por DanielFerreira

Dom Abr 12, 2015 16:10
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
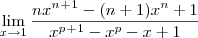 entao fiz o desenvolvimento e cheguei a a algo do tipo
entao fiz o desenvolvimento e cheguei a a algo do tipo 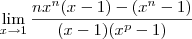 a partir dai nao achei termos em comum para cortar termos e chegar a uma reposta concreta se alguem souber agradeço
a partir dai nao achei termos em comum para cortar termos e chegar a uma reposta concreta se alguem souber agradeço 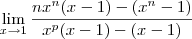 mas nao sai dai!!
mas nao sai dai!!
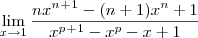 entao fiz o desenvolvimento e cheguei a a algo do tipo
entao fiz o desenvolvimento e cheguei a a algo do tipo 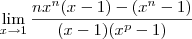 a partir dai nao achei termos em comum para cortar termos e chegar a uma reposta concreta se alguem souber agradeço
a partir dai nao achei termos em comum para cortar termos e chegar a uma reposta concreta se alguem souber agradeço 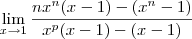 mas nao sai dai!!
mas nao sai dai!!
(...)
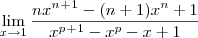 .
.a partir dai nao achei termos em comum para cortar termos e chegar a uma reposta
 :
:


 na hora de substituir a equação
na hora de substituir a equação  a resposta seria (x-1)(n) ja que sao n termos e multiplicando eles por 1 seria n a resposta dessa parte da equação?
a resposta seria (x-1)(n) ja que sao n termos e multiplicando eles por 1 seria n a resposta dessa parte da equação?
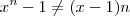 , são bem diferentes. Sobre seu limite, não vejo indeterminação quando
, são bem diferentes. Sobre seu limite, não vejo indeterminação quando  . Você tentou substituir? Tem a resposta?
. Você tentou substituir? Tem a resposta?

 ai o produto notavel disso
ai o produto notavel disso  e substituindo o 1 no lugar de x eu acharei n termos que sao 1 elevado a um valor n que independente dele vai dar um sendo assim terrei
e substituindo o 1 no lugar de x eu acharei n termos que sao 1 elevado a um valor n que independente dele vai dar um sendo assim terrei  que sera n!
que sera n!

 para posteriormente poder cortar com a expressao de baixo, pois se nao o limite fica indeterminado!
para posteriormente poder cortar com a expressao de baixo, pois se nao o limite fica indeterminado!
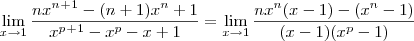
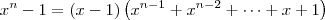
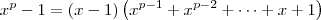
![\lim_{ x\to1}\frac{nx^n(x-1)-(x^n-1)}{(x-1)(x^p-1)} = \lim_{ x\to1}\frac{(x-1)\left[nx^n - \left(x^{n-1} + x^{n-2} + \cdots + x + 1\right)\right]}{(x-1)(x - 1)\left(x^{p-1} + x^{p-2} + \cdots + x + 1\right)} \lim_{ x\to1}\frac{nx^n(x-1)-(x^n-1)}{(x-1)(x^p-1)} = \lim_{ x\to1}\frac{(x-1)\left[nx^n - \left(x^{n-1} + x^{n-2} + \cdots + x + 1\right)\right]}{(x-1)(x - 1)\left(x^{p-1} + x^{p-2} + \cdots + x + 1\right)}](/latexrender/pictures/6315765ec26517366e19bd4a290eb47c.png)
![\lim_{ x\to1}\frac{(x-1)\left[nx^n - \left(x^{n-1} + x^{n-2} + \cdots + x + 1\right)\right]}{(x-1)(x - 1)\left(x^{p-1} + x^{p-2} + \cdots + x + 1\right)} = \lim_{ x\to1}\frac{nx^n - \left(x^{n-1} + x^{n-2} + \cdots + x + 1\right)}{(x - 1)\left(x^{p-1} + x^{p-2} + \cdots + x + 1\right)} \lim_{ x\to1}\frac{(x-1)\left[nx^n - \left(x^{n-1} + x^{n-2} + \cdots + x + 1\right)\right]}{(x-1)(x - 1)\left(x^{p-1} + x^{p-2} + \cdots + x + 1\right)} = \lim_{ x\to1}\frac{nx^n - \left(x^{n-1} + x^{n-2} + \cdots + x + 1\right)}{(x - 1)\left(x^{p-1} + x^{p-2} + \cdots + x + 1\right)}](/latexrender/pictures/72087ff4960c88c45af3d09b3639c776.png)
 .
. por
por  resulta em
resulta em  .
. por
por  . Aplicando os conhecimentos sobre divisão de polinômios, obtemos:
. Aplicando os conhecimentos sobre divisão de polinômios, obtemos:![\left[nx^n - \left(x^{n-1} + x^{n-2} + \cdots + x + 1\right)\right] \div (x - 1) \left[nx^n - \left(x^{n-1} + x^{n-2} + \cdots + x + 1\right)\right] \div (x - 1)](/latexrender/pictures/941b7d8ce45174ec7dc2579fd8c2b22e.png)
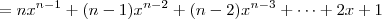

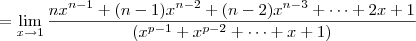
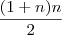 .
.







