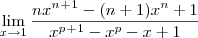 entao fiz o desenvolvimento e cheguei a a algo do tipo
entao fiz o desenvolvimento e cheguei a a algo do tipo 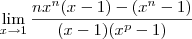 a partir dai nao achei termos em comum para cortar termos e chegar a uma reposta concreta se alguem souber agradeço
a partir dai nao achei termos em comum para cortar termos e chegar a uma reposta concreta se alguem souber agradeço eu cheguei a outra fatoração tbm que h
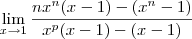 mas nao sai dai!!
mas nao sai dai!!
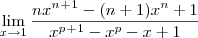 entao fiz o desenvolvimento e cheguei a a algo do tipo
entao fiz o desenvolvimento e cheguei a a algo do tipo 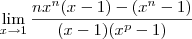 a partir dai nao achei termos em comum para cortar termos e chegar a uma reposta concreta se alguem souber agradeço
a partir dai nao achei termos em comum para cortar termos e chegar a uma reposta concreta se alguem souber agradeço 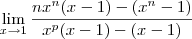 mas nao sai dai!!
mas nao sai dai!!
giulioaltoe escreveu:a questao e essa(...)
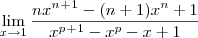 .
.giulioaltoe escreveu:fiz o desenvolvimento e cheguei a a algo do tipoa partir dai nao achei termos em comum para cortar termos e chegar a uma reposta
 :
:

giulioaltoe escreveu:eu tenho uma potencia com radical indefinido como posso saber ate onde devo fazer o produto notavel, existe alguma propriedade que resuma isso!?

 na hora de substituir a equação
na hora de substituir a equação  a resposta seria (x-1)(n) ja que sao n termos e multiplicando eles por 1 seria n a resposta dessa parte da equação?
a resposta seria (x-1)(n) ja que sao n termos e multiplicando eles por 1 seria n a resposta dessa parte da equação?
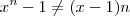 , são bem diferentes. Sobre seu limite, não vejo indeterminação quando
, são bem diferentes. Sobre seu limite, não vejo indeterminação quando  . Você tentou substituir? Tem a resposta?
. Você tentou substituir? Tem a resposta?

 ai o produto notavel disso
ai o produto notavel disso  e substituindo o 1 no lugar de x eu acharei n termos que sao 1 elevado a um valor n que independente dele vai dar um sendo assim terrei
e substituindo o 1 no lugar de x eu acharei n termos que sao 1 elevado a um valor n que independente dele vai dar um sendo assim terrei  que sera n!
que sera n!

 para posteriormente poder cortar com a expressao de baixo, pois se nao o limite fica indeterminado!
para posteriormente poder cortar com a expressao de baixo, pois se nao o limite fica indeterminado!
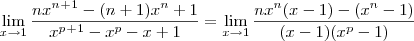
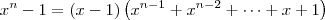
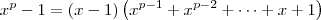
![\lim_{ x\to1}\frac{nx^n(x-1)-(x^n-1)}{(x-1)(x^p-1)} = \lim_{ x\to1}\frac{(x-1)\left[nx^n - \left(x^{n-1} + x^{n-2} + \cdots + x + 1\right)\right]}{(x-1)(x - 1)\left(x^{p-1} + x^{p-2} + \cdots + x + 1\right)} \lim_{ x\to1}\frac{nx^n(x-1)-(x^n-1)}{(x-1)(x^p-1)} = \lim_{ x\to1}\frac{(x-1)\left[nx^n - \left(x^{n-1} + x^{n-2} + \cdots + x + 1\right)\right]}{(x-1)(x - 1)\left(x^{p-1} + x^{p-2} + \cdots + x + 1\right)}](/latexrender/pictures/6315765ec26517366e19bd4a290eb47c.png)
![\lim_{ x\to1}\frac{(x-1)\left[nx^n - \left(x^{n-1} + x^{n-2} + \cdots + x + 1\right)\right]}{(x-1)(x - 1)\left(x^{p-1} + x^{p-2} + \cdots + x + 1\right)} = \lim_{ x\to1}\frac{nx^n - \left(x^{n-1} + x^{n-2} + \cdots + x + 1\right)}{(x - 1)\left(x^{p-1} + x^{p-2} + \cdots + x + 1\right)} \lim_{ x\to1}\frac{(x-1)\left[nx^n - \left(x^{n-1} + x^{n-2} + \cdots + x + 1\right)\right]}{(x-1)(x - 1)\left(x^{p-1} + x^{p-2} + \cdots + x + 1\right)} = \lim_{ x\to1}\frac{nx^n - \left(x^{n-1} + x^{n-2} + \cdots + x + 1\right)}{(x - 1)\left(x^{p-1} + x^{p-2} + \cdots + x + 1\right)}](/latexrender/pictures/72087ff4960c88c45af3d09b3639c776.png)
 .
. por
por  resulta em
resulta em  .
. por
por  . Aplicando os conhecimentos sobre divisão de polinômios, obtemos:
. Aplicando os conhecimentos sobre divisão de polinômios, obtemos:![\left[nx^n - \left(x^{n-1} + x^{n-2} + \cdots + x + 1\right)\right] \div (x - 1) \left[nx^n - \left(x^{n-1} + x^{n-2} + \cdots + x + 1\right)\right] \div (x - 1)](/latexrender/pictures/941b7d8ce45174ec7dc2579fd8c2b22e.png)
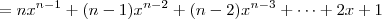

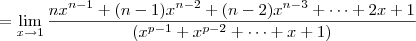
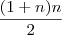 .
.


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes

 .
.
 :
: