 por Claudin » Qua Jun 29, 2011 22:14
por Claudin » Qua Jun 29, 2011 22:14
Alguém poderia ajudar na resolução do exercício.
![\lim_{x\rightarrow2}\frac{\sqrt[3]{x}-\sqrt[3]{2}}{x-2} \lim_{x\rightarrow2}\frac{\sqrt[3]{x}-\sqrt[3]{2}}{x-2}](/latexrender/pictures/ac4411aab556984732118746ecfb686b.png)
obs: resolver pela definição
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Fabio Cabral » Qui Jun 30, 2011 11:29
por Fabio Cabral » Qui Jun 30, 2011 11:29
Você tem a opção de resolver aplicando L'Hopital. Indeterminação do tipo

" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por Claudin » Qui Jun 30, 2011 11:48
por Claudin » Qui Jun 30, 2011 11:48
Gostaria de resolver sem aplicar o L'Hopital como manda o exercício!
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Qui Jun 30, 2011 11:50
por LuizAquino » Qui Jun 30, 2011 11:50
Qual é o texto completo e original do exercício?
DicaUtilizando produtos notáveis, note que:
![x - 2 = {\sqrt[3]{x}}^3 - {\sqrt[3]{2}}^3 = \left(\sqrt[3]{x} - \sqrt[3]{2}\right)\left(\sqrt[3]{x^2} + \sqrt[3]{x}\sqrt[3]{2} + \sqrt[3]{2^2}\right) x - 2 = {\sqrt[3]{x}}^3 - {\sqrt[3]{2}}^3 = \left(\sqrt[3]{x} - \sqrt[3]{2}\right)\left(\sqrt[3]{x^2} + \sqrt[3]{x}\sqrt[3]{2} + \sqrt[3]{2^2}\right)](/latexrender/pictures/f4c2504cc27d7f8bacdf9b3c47f4d8ce.png)
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Qui Jun 30, 2011 12:03
por Claudin » Qui Jun 30, 2011 12:03
Resolver pela definição o limite dado:
Este é o enunciado!
Como você elevou ao quadrado os dois termos? Só pra cair em produto notável?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Qui Jun 30, 2011 12:14
por LuizAquino » Qui Jun 30, 2011 12:14
Coisa alguma foi "elevada ao quadrado".
A ideia é usar o produto notável:

.
Temos a expressão
x - 2. Como fazer aparecer a diferença entre cubos, mas sem alterar o valor da expressão original? Ora, basta usar o fato de que
![\sqrt[3]{a}^3 = a \sqrt[3]{a}^3 = a](/latexrender/pictures/858c1d8586c8269b9be16a8fd2370d91.png)
. Ou seja, é válido que
![x - 2 = \sqrt[3]{x}^3 - \sqrt[3]{2}^3 x - 2 = \sqrt[3]{x}^3 - \sqrt[3]{2}^3](/latexrender/pictures/77a1645b35957c51a2ac807b67c6e40f.png)
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Qui Jun 30, 2011 12:22
por Claudin » Qui Jun 30, 2011 12:22
Correto Luiz.

"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Fabio Cabral » Qui Jun 30, 2011 13:42
por Fabio Cabral » Qui Jun 30, 2011 13:42
![\lim_{x\rightarrow2}\frac{\sqrt[3]{x}-\sqrt[3]{2}}{(\sqrt[3]{x}-\sqrt[3]{2}).(\sqrt[3]{x^2}+\sqrt[3]{x}.\sqrt[3]{2}+\sqrt[3]{2^2})} = \lim_{x\rightarrow2}\frac{1}{(\sqrt[3]{x^2}+\sqrt[3]{x}.\sqrt[3]{2}+\sqrt[3]{2^2})} = \frac{1}{3\sqrt[3]{2^2}} \lim_{x\rightarrow2}\frac{\sqrt[3]{x}-\sqrt[3]{2}}{(\sqrt[3]{x}-\sqrt[3]{2}).(\sqrt[3]{x^2}+\sqrt[3]{x}.\sqrt[3]{2}+\sqrt[3]{2^2})} = \lim_{x\rightarrow2}\frac{1}{(\sqrt[3]{x^2}+\sqrt[3]{x}.\sqrt[3]{2}+\sqrt[3]{2^2})} = \frac{1}{3\sqrt[3]{2^2}}](/latexrender/pictures/ae69d1cd879c54b66bc749a9b43862fd.png)
ou
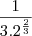
Correto?
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por Claudin » Qui Jun 30, 2011 14:46
por Claudin » Qui Jun 30, 2011 14:46
Corretíssimo Fábio

Esta explicação que eu esperava.
Abraço
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Qui Jun 30, 2011 20:26
por Claudin » Qui Jun 30, 2011 20:26
Não seria pela definição não Marcelo
olhei enunciado errado. Seria calcular desse modo sem usar L'Hopital
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6640 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4786 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5114 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7249 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4429 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow2}\frac{\sqrt[3]{x}-\sqrt[3]{2}}{x-2} \lim_{x\rightarrow2}\frac{\sqrt[3]{x}-\sqrt[3]{2}}{x-2}](/latexrender/pictures/ac4411aab556984732118746ecfb686b.png)

![\lim_{x\rightarrow2}\frac{\sqrt[3]{x}-\sqrt[3]{2}}{x-2} \lim_{x\rightarrow2}\frac{\sqrt[3]{x}-\sqrt[3]{2}}{x-2}](/latexrender/pictures/ac4411aab556984732118746ecfb686b.png)




![x - 2 = {\sqrt[3]{x}}^3 - {\sqrt[3]{2}}^3 = \left(\sqrt[3]{x} - \sqrt[3]{2}\right)\left(\sqrt[3]{x^2} + \sqrt[3]{x}\sqrt[3]{2} + \sqrt[3]{2^2}\right) x - 2 = {\sqrt[3]{x}}^3 - {\sqrt[3]{2}}^3 = \left(\sqrt[3]{x} - \sqrt[3]{2}\right)\left(\sqrt[3]{x^2} + \sqrt[3]{x}\sqrt[3]{2} + \sqrt[3]{2^2}\right)](/latexrender/pictures/f4c2504cc27d7f8bacdf9b3c47f4d8ce.png)


 .
.![\sqrt[3]{a}^3 = a \sqrt[3]{a}^3 = a](/latexrender/pictures/858c1d8586c8269b9be16a8fd2370d91.png) . Ou seja, é válido que
. Ou seja, é válido que ![x - 2 = \sqrt[3]{x}^3 - \sqrt[3]{2}^3 x - 2 = \sqrt[3]{x}^3 - \sqrt[3]{2}^3](/latexrender/pictures/77a1645b35957c51a2ac807b67c6e40f.png) .
.







