Indução Matemática - Dúvidas

por **Jucassaba** » Qua Dez 10, 2008 11:43

Caros amigos,
estou sem entender como o examinador desenvolvel este caso, para ser bem expecífico, a duvida é no desenvolvimento da 2a para a 3a linha do passo indutivo, quando desenvolve o 1o. termo de P(k+1).

abaixo a proposição:

$\sum_{i=1}^{n}i\left(i+1 \right)=\frac{1}{3}n\left(n+1 \right)\left(n+2 \right)\;\; \forall \:n\in N$

Não há o que se falar com relação a Base da Indução para P(n) verdadeira onde n=1.
Na HIpótese Indutiva também não tenho dúvidas com relação a P(k) verdadeira para $k\geq1$ .
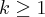
Agora no Passo Indutivo eu não consegui enteder o desenvolvimento da 2a para a 3a linha.

Desenvolvo o primeiro termo de P(k+1) e aplico a hipótese indutiva.

$\sum_{i=1}^{k+1}i\left(i+1 \right)\;\;\rightarrow \;\; \frac{1}{3}\left(k+1 \right)\left(\left(k+1 \right)+1 \right)\left(\left( k+1 \right)+2 \right)$

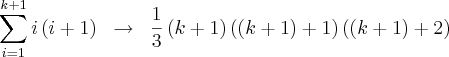
até aqui, claro, tudo bem...

$\rightarrow \;\;\; \frac{1}{3}k \left(k+1 \right)\left(k+2 \right)+ \left( k+1 \right)\left( k+2 \right)$

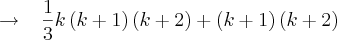
da linha acima para esta seguinte q não entendo com foi feito o desenvolvimento.

$\left(k+1 \right)\left(k+2 \right) \left( \frac{k}{3}+1 \right)$

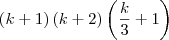
a simplifição acima não entendi. Entao fiquei inseguro para a ultima linha abaixo, que conclui o desenvolvimento do primeiro termo.

$\frac{1}{3}\left(k+1 \right)\left(k+2 \right) \left(k+3 \right)$

No desenvolimento do segundo termo de P(k+1) não tenho dúvidas. Está Ok.
Se os amigos puderem me ajudar eu agradeço.

Abraços Juca

por **felipe correa** » Qua Dez 10, 2008 19:29

Na expressão:

$\frac{1}{3}k(k+1)(k+2)+(k+1)(k+2)$

O termo (k+1)(k+2) foi colocado em evidencia:

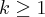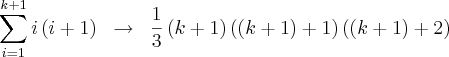
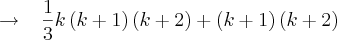
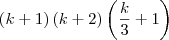
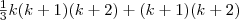
$\frac{1}{3}k(k+1)(k+2)+(k+1)(k+2) = (k+1)(k+2)\left[\frac{\frac{1}{3}k(k+1)(k+2)}{(k+1)(k+2)}+\frac{(k+1)(k+2)}{(k+1)(k+2)}\right]$

$(k+1)(k+2)\left[\frac{\frac{1}{3}k(k+1)(k+2)}{(k+1)(k+2)}+\frac{(k+1)(k+2)}{(k+1)(k+2)}\right]=(k+1)(k+2)\left(\frac{1}{3}k + 1\right)$