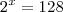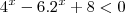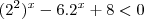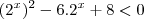Alguém poderia me ajudar a responder esses exercícios.?

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Alguém poderia me ajudar a responder esses exercícios.?

Regras do fórum
Responder

Alguém poderia me ajudar a responder esses exercícios.?

Mensagempor icarowilliams15 » Seg Jun 13, 2011 12:12

1. Construir os gráficos cartesianos das seguintes funções exponenciais
a).y=3^x
b).y=(1/3)^x
c).y=4^x
d).y=10^x
e).y=10^-x
f).y=(1/e)^x

2.2. Resolver as equações exponenciais abaixo:

a.2^x=128 b.3^x=243 c.2^x=1/16

d.(1/5)^x


3. Resolver as seguintes inequações exponenciais:

a.4^x-6.2^x+8<0 b.9^x-4.3^x+1+18>0 c.5^2x+1-26.5^x+5?0

d.2^2x-3^x+1>3^x-3 e.3^2x-3^x+1>3x-3 f.2^x(2^x+1)<2

4. Classificar as seguintes sentenças em verdadeiro ou falso, justificando:
a.3^2.7>1 b.(4/5)^-1.5>1 c.(0.3)^0.2>1

sao questoes de um exercicio de faculdade valendo pontos,quem poder me ajudar agraderia muito.
icarowilliams15
Novo Usuário
Novo Usuário
 
Mensagens: 8
Registrado em: Qua Mai 18, 2011 15:20
Formação Escolar: GRADUAÇÃO
Área/Curso: contabilidade
Andamento: cursando
Voltar ao topo

Re: Alguém poderia me ajudar a responder esses exercícios.?

Mensagempor Molina » Seg Jun 13, 2011 20:49

Boa noite.

Para sua primeira questão você pode dar valores para x e obter o valor de y aproximado. Ou então fazer o gráfico com o auxílio do wolframalpha.


Sua segunda questão vou fazer a letra a) e as outras são feitas de forma análoga:

2^x=128

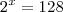fatorando o 128...

2^x=2^7

x=7


Na terceira questão o procedimento é parecido no que feito na questão anterior, com alguns detalhes. Vou fazer a letra a) o restante é análogo:

4^x-6.2^x+8<0

(2^2)^x-6.2^x+8<0

(2^x)^2-6.2^x+8<0

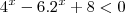
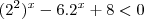
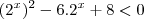Chamando 2^x = y...

y^2-6.y+8<0

Agora você resolve esta inequação do 2º grau normalmente. Não esqueça de voltar em 2^x = y e obter o intervalo em x.


A notação de sua quarta e última questão eu não entendi muito bem. Poderia ser mais claro?


Qualquer dúvida, avise! :y:
Diego Molina | CV | FB | .COM
Equipe AjudaMatemática.com


"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
Avatar do usuário
Molina
Colaborador Moderador - Professor
Colaborador Moderador - Professor
 
Mensagens: 1551
Registrado em: Dom Jun 01, 2008 14:10
Formação Escolar: GRADUAÇÃO
Área/Curso: Licenciatura em Matemática - UFSC
Andamento: formado
Voltar ao topo

Re: Alguém poderia me ajudar a responder esses exercícios.?

Mensagempor Claudin » Seg Jun 13, 2011 22:09

A nº 1 eu tinha explicado a teoria básica para ele mais cedo
com a teoria, ja da pra diferenciar os tipos de gráficos e estipular os valores.

Na última questão também não consegui compreender!
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
Claudin
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 913
Registrado em: Qui Mai 12, 2011 17:34
Formação Escolar: GRADUAÇÃO
Área/Curso: Engenharia Elétrica
Andamento: cursando
Voltar ao topo

Re: Alguém poderia me ajudar a responder esses exercícios.?

Mensagempor icarowilliams15 » Ter Jun 14, 2011 11:22

Molina escreveu:Boa noite.

Para sua primeira questão você pode dar valores para x e obter o valor de y aproximado. Ou então fazer o gráfico com o auxílio do wolframalpha.


Sua segunda questão vou fazer a letra a) e as outras são feitas de forma análoga:

2^x=128

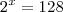fatorando o 128...

2^x=2^7

x=7


Na terceira questão o procedimento é parecido no que feito na questão anterior, com alguns detalhes. Vou fazer a letra a) o restante é análogo:

4^x-6.2^x+8<0

(2^2)^x-6.2^x+8<0

(2^x)^2-6.2^x+8<0

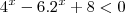
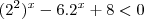
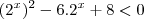Chamando 2^x = y...

y^2-6.y+8<0

Agora você resolve esta inequação do 2º grau normalmente. Não esqueça de voltar em 2^x = y e obter o intervalo em x.


A notação de sua quarta e última questão eu não entendi muito bem. Poderia ser mais claro?


Qualquer dúvida, avise! :y:



claudin vc tem msn?,da pra vc ficar online la no chat agora? pra vc entender muito bem essa 4ª questão.eu posso te enviar essas questoes pra seu email,desde ja aguardo.
icarowilliams15
Novo Usuário
Novo Usuário
 
Mensagens: 8
Registrado em: Qua Mai 18, 2011 15:20
Formação Escolar: GRADUAÇÃO
Área/Curso: contabilidade
Andamento: cursando
Voltar ao topo

Re: Alguém poderia me ajudar a responder esses exercícios.?

Mensagempor icarowilliams15 » Ter Jun 14, 2011 13:06

icarowilliams15 escreveu:
Molina escreveu:Boa noite.

Para sua primeira questão você pode dar valores para x e obter o valor de y aproximado. Ou então fazer o gráfico com o auxílio do wolframalpha.


Sua segunda questão vou fazer a letra a) e as outras são feitas de forma análoga:

2^x=128

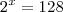fatorando o 128...

2^x=2^7

x=7


Na terceira questão o procedimento é parecido no que feito na questão anterior, com alguns detalhes. Vou fazer a letra a) o restante é análogo:

4^x-6.2^x+8<0

(2^2)^x-6.2^x+8<0

(2^x)^2-6.2^x+8<0

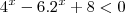
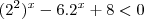
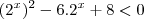Chamando 2^x = y...

y^2-6.y+8<0

Agora você resolve esta inequação do 2º grau normalmente. Não esqueça de voltar em 2^x = y e obter o intervalo em x.


A notação de sua quarta e última questão eu não entendi muito bem. Poderia ser mais claro?


Qualquer dúvida, avise! :y:



claudin vc tem msn?,da pra vc ficar online la no chat agora? pra vc entender muito bem essa 4ª questão.eu posso te enviar essas questoes pra seu email,desde ja aguardo.


pode responder as outras letras do 3ª e a d) a e) e a f) do 2ª,porque o 1 ja respondir e o 4ª ainda nao....mais depois vejo
icarowilliams15
Novo Usuário
Novo Usuário
 
Mensagens: 8
Registrado em: Qua Mai 18, 2011 15:20
Formação Escolar: GRADUAÇÃO
Área/Curso: contabilidade
Andamento: cursando
Voltar ao topo

Re: Alguém poderia me ajudar a responder esses exercícios.?

Mensagempor Claudin » Ter Jun 14, 2011 14:32

Pode mandar via e-mail Icaro
Mas aconselho a utilizar o "Latex", vai no editor de fórmulas para facilitar o entendimento
dos demais membros do fórum.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
Claudin
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 913
Registrado em: Qui Mai 12, 2011 17:34
Formação Escolar: GRADUAÇÃO
Área/Curso: Engenharia Elétrica
Andamento: cursando
Voltar ao topo

Re: Alguém poderia me ajudar a responder esses exercícios.?

Mensagempor icarowilliams15 » Ter Jun 14, 2011 16:02

certo,responde pra mim aí agora,preciso até as 16:00 o 3) e essas outras e) e f) do 2.que nao tinha colocado
(3?2)^x=8
(4?3)x=3?9
tenta aí..desde ja agradeço.
icarowilliams15
Novo Usuário
Novo Usuário
 
Mensagens: 8
Registrado em: Qua Mai 18, 2011 15:20
Formação Escolar: GRADUAÇÃO
Área/Curso: contabilidade
Andamento: cursando
Voltar ao topo

Re: Alguém poderia me ajudar a responder esses exercícios.?

Mensagempor icarowilliams15 » Qua Jun 15, 2011 10:57

claudin me passa seu email então,vou enviar um segundo exercicio sobre logaritmo no seu email,anexado do word ja com as formulas...aguado.!
icarowilliams15
Novo Usuário
Novo Usuário
 
Mensagens: 8
Registrado em: Qua Mai 18, 2011 15:20
Formação Escolar: GRADUAÇÃO
Área/Curso: contabilidade
Andamento: cursando
Voltar ao topo
Responder

Voltar para Funções

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 


Tópico Popular

Assunto: método de contagem
Autor: sinuca147 - Seg Mai 25, 2009 09:10

Veja este exercício:

Se A = {x \in Z \hspace{1mm} | \hspace{1mm} \frac{20}{x} = n, n \in N} e B = {x \in R \hspace{1mm} | \hspace{1mm} x = 5m, m \in z}, então o número de elementos A \cap B é:

Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.

Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?

No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:

existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?

A resposta é 3?

Obrigado.

Assunto: método de contagem
Autor: Molina - Seg Mai 25, 2009 20:42

Boa noite, sinuca.

Se A = {x \in Z \hspace{1mm} | \hspace{1mm} \frac{20}{x} = n, n \in N} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é A = {1, 2, 4, 5, 10, 20}

Se B = {x \in R \hspace{1mm} | \hspace{1mm} x = 5m, m \in z} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...

Feito isso precisamos ver os números que está em ambos os conjuntos, que são: 5, 10 e 20 (3 valores, como você achou).

Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?

sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:

existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x

A resposta é 3? Sim, pelo menos foi o que vimos a cima


Bom estudo, :y:

Assunto: método de contagem
Autor: sinuca147 - Seg Mai 25, 2009 23:35

Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.

Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:

Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?

Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?


Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum