 por Fabio Cabral » Qui Jun 02, 2011 12:07
por Fabio Cabral » Qui Jun 02, 2011 12:07
Pessoal, tenho bastante dúvidas sobre qual regra usar.
Veja:
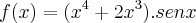
Usei a regra do produto: a'(x).b(x)+a(x).b'(x).
Obtive:

Eu posso aplicar a distributiva?
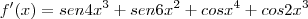 Teria que usar essa regra do produto mesmo?
Teria que usar essa regra do produto mesmo?Grato
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por Fabio Cabral » Qui Jun 02, 2011 14:42
por Fabio Cabral » Qui Jun 02, 2011 14:42
pessoal?
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por Charlys Couto » Qui Jun 02, 2011 15:58
por Charlys Couto » Qui Jun 02, 2011 15:58
E essa mesmo ...
-
Charlys Couto
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Abr 29, 2011 12:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Agronomica
- Andamento: cursando
 por Fabio Cabral » Qui Jun 02, 2011 19:35
por Fabio Cabral » Qui Jun 02, 2011 19:35
Certo.
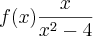
Aplicando a propriedade do Quociente:

Esse é realmente o Resultado?
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por LuizAquino » Qui Jun 02, 2011 19:47
por LuizAquino » Qui Jun 02, 2011 19:47
Fabio Cabral escreveu: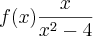
Aplicando a propriedade do Quociente:

Esse é realmente o Resultado?
Não.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Fabio Cabral » Sex Jun 03, 2011 11:22
por Fabio Cabral » Sex Jun 03, 2011 11:22
Ok, Luiz.
Tentei mais uma vez e cheguei em:

Muito errado ainda?
Grato.
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por LuizAquino » Sex Jun 03, 2011 12:15
por LuizAquino » Sex Jun 03, 2011 12:15
Fabio Cabral escreveu:Tentei mais uma vez e cheguei em:

Muito errado ainda?
Sim, está.
Eu recomendo que você envie a sua resolução para que possamos encontrar o erro.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Fabio Cabral » Sex Jun 03, 2011 12:31
por Fabio Cabral » Sex Jun 03, 2011 12:31
Eu mesmo o encontrei. O erro foi falta de Atenção.
Queria pedir a vocês aqui do fórum uma força no seguinte sentido.
Dizer se está certo ou não, pois estou querendo realmente SABER! E, para evitar criar vários tópicos repetidos, postarei somente nesse. Tudo bem?
1)

Usei a regra do produto para "montar" e para derivar, usei a regra da cadeia. Resultou em:

2)
![f(x) = \sqrt[3]{2x+1} f(x) = \sqrt[3]{2x+1}](/latexrender/pictures/c378ab0c2e7c876a13143191f861d47e.png)
Resultando em:

Certo?
Obrigado, galera !
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por LuizAquino » Sex Jun 03, 2011 14:29
por LuizAquino » Sex Jun 03, 2011 14:29
Fabio Cabral escreveu:Queria pedir a vocês aqui do fórum uma força no seguinte sentido.
Dizer se está certo ou não, pois estou querendo realmente SABER! E, para evitar criar vários tópicos repetidos, postarei somente nesse. Tudo bem?
Por que ao invés disso você não aprende a usar um Sistema Computacional Algébrico? Por exemplo o
SAGE,
Maple ou
Mathematica. Você pode usar esses programas para conferir as suas respostas.
Inclusive, alguns desses programas possuem versões que funcionam on-line. Por exemplo, viste:
http://www.sagenb.org/http://www.wolframalpha.com/
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Fabio Cabral » Sáb Jun 04, 2011 19:11
por Fabio Cabral » Sáb Jun 04, 2011 19:11
Certo, Luiz.
Já tinha aqui o Maple 13, porém, usava somente pra fazer gráficos e conferir limites.
Estou com dificuldade para montar a fórmula para descobrir a derivada. Como faço?
Por exemplo: Quero descobrir a derivada de X³, como escrevo isso de forma que o Maple entenda?
Att,
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por LuizAquino » Sáb Jun 04, 2011 21:10
por LuizAquino » Sáb Jun 04, 2011 21:10
Fabio Cabral escreveu:Por exemplo: Quero descobrir a derivada de X³, como escrevo isso de forma que o Maple entenda?
Eu tenho certeza que com uma rápida busca você pode encontrar milhares de páginas com tutoriais sobre o Maple!

Que tal procurar um pouco?

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Fabio Cabral » Dom Jun 05, 2011 16:03
por Fabio Cabral » Dom Jun 05, 2011 16:03
Certo. Dei uma olhada.
Veja:
![f(x)=\sqrt[3]{2x+1} f(x)=\sqrt[3]{2x+1}](/latexrender/pictures/787835e8fce173ac7e2b995ddd713e82.png)


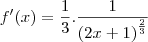
Fiz dessa forma, conforme o professor ensinou para tratar de raízes.
Só que, segunda Maple13 e Wolfram, o resultado é:

Não entendi da onde saiu esse 2 !
Grato
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por AlbertoAM » Dom Jun 05, 2011 19:55
por AlbertoAM » Dom Jun 05, 2011 19:55
Lembre-se que:

Ou seja, você teria que ter multiplicado a sua expressão pela derivada de (2x+1).
-
AlbertoAM
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Qui Nov 11, 2010 15:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Fabio Cabral » Dom Jun 05, 2011 20:02
por Fabio Cabral » Dom Jun 05, 2011 20:02
Realmente funcionou. Porém estou confundido as coisas..
Isto é a regra da cadeia?
Estou estranhando porque todas as questões que ele passou com raízes, nenhuma teve que ser multiplicada pela derivada de f(x). Ou seja, apenas passei para a forma de potência, descendo o expoente e subtraindo 1 do expoente.
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por AlbertoAM » Dom Jun 05, 2011 20:23
por AlbertoAM » Dom Jun 05, 2011 20:23
Sim, é a regra da cadeia.
Observe que:
Se

então

.Porém, se:
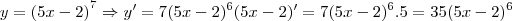
Ou, seja, não temos que mais que derivar apenas x, temos uma função composta, no caso acima (5x-2).
Observe também que:
![y=\sqrt[3]{cos^2x}={cosx}^{2/3}\Rightarrow y'=\frac{2}{3}{cosx}^{-1/3}(cosx)'=\frac{-2senx}{3\sqrt[3]{cosx}} y=\sqrt[3]{cos^2x}={cosx}^{2/3}\Rightarrow y'=\frac{2}{3}{cosx}^{-1/3}(cosx)'=\frac{-2senx}{3\sqrt[3]{cosx}}](/latexrender/pictures/6465cf5a4f2578720a52c952018b7f47.png)
Novamente, não temos apenas x dentro da raiz .
-
AlbertoAM
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Qui Nov 11, 2010 15:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por AlbertoAM » Dom Jun 05, 2011 20:25
por AlbertoAM » Dom Jun 05, 2011 20:25
AlbertoAM escreveu:Sim, é a regra da cadeia.
Observe que:
Se

então

.Porém, se:
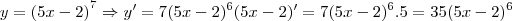
Ou, seja, não temos que mais que derivar apenas x, temos uma função composta, no caso acima (5x-2).
Observe também que:
![y=\sqrt[3]{cos^2x}={(cosx)}^{2/3}\Rightarrow y'=\frac{2}{3}{(cosx)}^{-1/3}(cosx)'=\frac{-2senx}{3\sqrt[3]{cosx}} y=\sqrt[3]{cos^2x}={(cosx)}^{2/3}\Rightarrow y'=\frac{2}{3}{(cosx)}^{-1/3}(cosx)'=\frac{-2senx}{3\sqrt[3]{cosx}}](/latexrender/pictures/12f8ae61f26a0c5a593d044c0f0f29a1.png)
Novamente, não temos apenas x dentro da raiz .
-
AlbertoAM
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Qui Nov 11, 2010 15:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Fabio Cabral » Dom Jun 05, 2011 21:17
por Fabio Cabral » Dom Jun 05, 2011 21:17
Muito bom, Alberto. Muito obrigado mesmo ! Mais dúvidas virão ! hehe
Abraço
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por Fabio Cabral » Dom Jun 05, 2011 21:48
por Fabio Cabral » Dom Jun 05, 2011 21:48
Vejamos a seguinte função:
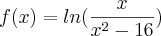
Ultilizarei a Regra da Cadeia?
Derivei a fração do logaritmando e encontrei:
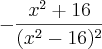
Se seguir a regra da cadeia, terei que derivar primeiro Log e depois multiplicar pela Fração interna.
Fiz da seguinte maneira pra achar o f'(x)Log:

Depois disso tenho que multiplicar pela função interna novamente?
Não estou conseguindo resolver essa derivada !
Grato
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por AlbertoAM » Seg Jun 06, 2011 22:52
por AlbertoAM » Seg Jun 06, 2011 22:52
Sim, você terá que usar novamente a Regra da Cadeia.Estou sem tempo para escrever usando o latex, então eu escaneei o que fiz no papel.
Está aqui:
Espero que entenda.
-
AlbertoAM
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Qui Nov 11, 2010 15:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Fabio Cabral » Ter Jun 07, 2011 14:09
por Fabio Cabral » Ter Jun 07, 2011 14:09
Entendi sim. Mas pra mim, esse tipo de simplificação não podia ser feito !
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por Fabio Cabral » Ter Jun 07, 2011 14:24
por Fabio Cabral » Ter Jun 07, 2011 14:24
Agora, uma questão aparentemente fácil, mas que estou tendo dificuldades pra encontrar um resultado que bata com o gabarito.
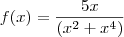
:
Apliquei a regra do quociente só que não bate com o resultado que é:
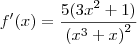
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por AlbertoAM » Ter Jun 07, 2011 16:39
por AlbertoAM » Ter Jun 07, 2011 16:39
Porque a simplicação não poderia ter sido feita?
Quanto ao exercíco:
![f'(x)=5\left[\frac{x^2+x^4-x(2x+4x^3)}{(x^2+x^4)^2}\right]=5\left[\frac{-3x^4-x^2}{x^8+2x^6+x^4} \right]=\\\\5\left[\left\frac{-x^2(3x^2+1)}{x^2(x^6+2x^4+x^2)}\right]=\frac{-5(3x^2+1)}{(x^3+x)^2} f'(x)=5\left[\frac{x^2+x^4-x(2x+4x^3)}{(x^2+x^4)^2}\right]=5\left[\frac{-3x^4-x^2}{x^8+2x^6+x^4} \right]=\\\\5\left[\left\frac{-x^2(3x^2+1)}{x^2(x^6+2x^4+x^2)}\right]=\frac{-5(3x^2+1)}{(x^3+x)^2}](/latexrender/pictures/6fa94e05baad0c7233a9c072aceaa339.png)
Verifique se não é -5 no gabarito por favor.
-
AlbertoAM
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Qui Nov 11, 2010 15:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Fabio Cabral » Qua Jun 08, 2011 10:10
por Fabio Cabral » Qua Jun 08, 2011 10:10
Sim, realmente é - 5.
Agora, não consegui compreender porque o 5 multiplicou todo mundo!
Eu derivei pela regra do quociente da seguinte forma:
N(x) = 5x -> N'(x) = 5
D(x) = (x²+x^4) -> D'(x) = 2x+4x^3
E joguei na regra.
Porque esse 5?
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por AlbertoAM » Qua Jun 08, 2011 15:16
por AlbertoAM » Qua Jun 08, 2011 15:16
Como o 5 é uma constante, podemos "tirar" ele da derivada.Do mesmo jeito que poderíamos ter derivado como 5x, daria na mesma, mas teríamos mais contas.
-
AlbertoAM
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Qui Nov 11, 2010 15:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivadas] Dificuldade para calcular derivadas CDI 1
por srmai » Seg Nov 04, 2013 01:21
- 0 Respostas
- 2260 Exibições
- Última mensagem por srmai

Seg Nov 04, 2013 01:21
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Interpretação de derivadas e funções
por vinik1 » Qua Out 12, 2011 16:03
- 5 Respostas
- 7465 Exibições
- Última mensagem por vinik1

Qui Out 13, 2011 10:48
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Derivadas em pontos dados
por MarlonMO250 » Sex Mar 01, 2013 21:02
- 6 Respostas
- 4938 Exibições
- Última mensagem por Russman

Sáb Mar 02, 2013 03:42
Cálculo: Limites, Derivadas e Integrais
-
- (derivadas) derivadas com raiz como se faz
por jana garcia » Qua Jun 25, 2014 00:28
- 1 Respostas
- 2960 Exibições
- Última mensagem por e8group

Qua Jun 25, 2014 01:13
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Derivadas com definição de limites
 por concurseironf » Sex Set 05, 2014 18:11
por concurseironf » Sex Set 05, 2014 18:11
- 1 Respostas
- 1988 Exibições
- Última mensagem por DanielFerreira

Dom Set 07, 2014 22:18
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

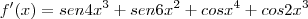

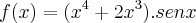

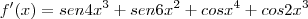





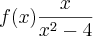








![f(x) = \sqrt[3]{2x+1} f(x) = \sqrt[3]{2x+1}](/latexrender/pictures/c378ab0c2e7c876a13143191f861d47e.png)






![f(x)=\sqrt[3]{2x+1} f(x)=\sqrt[3]{2x+1}](/latexrender/pictures/787835e8fce173ac7e2b995ddd713e82.png)


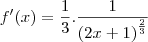





 então
então  .Porém, se:
.Porém, se: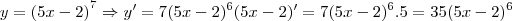
![y=\sqrt[3]{cos^2x}={cosx}^{2/3}\Rightarrow y'=\frac{2}{3}{cosx}^{-1/3}(cosx)'=\frac{-2senx}{3\sqrt[3]{cosx}} y=\sqrt[3]{cos^2x}={cosx}^{2/3}\Rightarrow y'=\frac{2}{3}{cosx}^{-1/3}(cosx)'=\frac{-2senx}{3\sqrt[3]{cosx}}](/latexrender/pictures/6465cf5a4f2578720a52c952018b7f47.png)

então
.Porém, se:


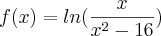
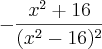




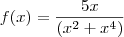 :
: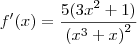

![f'(x)=5\left[\frac{x^2+x^4-x(2x+4x^3)}{(x^2+x^4)^2}\right]=5\left[\frac{-3x^4-x^2}{x^8+2x^6+x^4} \right]=\\\\5\left[\left\frac{-x^2(3x^2+1)}{x^2(x^6+2x^4+x^2)}\right]=\frac{-5(3x^2+1)}{(x^3+x)^2} f'(x)=5\left[\frac{x^2+x^4-x(2x+4x^3)}{(x^2+x^4)^2}\right]=5\left[\frac{-3x^4-x^2}{x^8+2x^6+x^4} \right]=\\\\5\left[\left\frac{-x^2(3x^2+1)}{x^2(x^6+2x^4+x^2)}\right]=\frac{-5(3x^2+1)}{(x^3+x)^2}](/latexrender/pictures/6fa94e05baad0c7233a9c072aceaa339.png)








