Se os lados de um triângulo medem x, x+1 e x+2, então, para qualquer x real e maior que 1, o cosseno do maior ângulo interno desse triângulo é igual a:
Eu fiz assim...
O maior ângulo interno é o que se opõe ao maior lado, logo, ângulo oposto a x+2.
Sendo assim, pela lei dos cossenos, sendo alpha o maior ângulo interno deste triângulo...

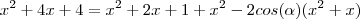

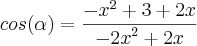
No meu livro a resposta é
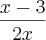 ...
...Agradeço desde já!










![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)