 por jamiel » Qua Mai 25, 2011 14:27
por jamiel » Qua Mai 25, 2011 14:27
Os biólogos observaram que a taxa de canto dos grilos em uma certa espécie aparentemente
está relacionada com a temperatura. A tabela a seguir mostra as taxas de canto para várias temperaturas.
T(Fº) |50 |55 |60 |65 |70
Taxa |16 |41 |79 |102 |135
a)Faça um gráfico e identifique o modelo que melhor se ajusta aos dados.
b)Encontre uma equação que representa o modelo.
c)IUse o modelo encontrado para estimar a taxa de canto a 100º
O gráfico está no arquivo em JPG anexado ao post.
O modelo, a primeira olhada, é uma função do tipo y = ax + b, até aí, tudo bem. Mas o problema é q não estou conseguindo encontrar uma equação q englobe todos os períodos do gráfico. Já tentei equação da reta e tudo mais, mas não tow conseguindo. Se eu fizer um sistema por período, até consigo, mas apenas para os valores deste período. Como seria essa equação, como é pedido no enunciado na letra "b)"?
Alguém para dar uma dica?
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por demolot » Qua Mai 25, 2011 16:25
por demolot » Qua Mai 25, 2011 16:25
Como nao pede analiticamente, voce poderia por esses valores na calculadora e ela dava-lhe e equaçao da recta muito rapido, mas ha a maneira analítica de fazer,
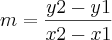
tomando como x a Temperatura e y a Taxa
-
demolot
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Sáb Dez 11, 2010 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Informatica
- Andamento: cursando
 por jamiel » Qua Mai 25, 2011 18:23
por jamiel » Qua Mai 25, 2011 18:23
Pois, é. Como eu disse antes, eu fiz a equação da reta, 119/20, mas fica impreciso, não tem como eu fazer uma função "geral" para todo o gráfico. Alguns valores batem, mas aproximados, não certinho. Agora, seu fizer por período, sim, aí dá certo. É isso q está me deixando com a pulga atr ás da orelha!
vlw ...
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por MarceloFantini » Qua Mai 25, 2011 23:40
por MarceloFantini » Qua Mai 25, 2011 23:40
identifique o modelo que melhor se ajusta aos dados
Isso não quer dizer "encontre uma curva que passe por todos os pontos". É possível, mas não quer dizer que é a melhor curva. Prosseguir com a sua idéia de manter uma reta é o caminho a se tomar, mas não se preocupe se nem todos os pontos estiverem nela: o importante é que o desvio da reta em relação a esses pontos seja pequeno.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calcular periodos de uma funcao
por explod1ng » Sáb Mar 27, 2010 21:07
- 0 Respostas
- 1071 Exibições
- Última mensagem por explod1ng

Sáb Mar 27, 2010 21:07
Funções
-
- questão função
por sheila » Qui Set 06, 2007 22:37
- 4 Respostas
- 7824 Exibições
- Última mensagem por admin

Ter Set 11, 2007 16:39
Funções
-
- Questão de Funçao
por kael » Qui Mar 05, 2009 16:30
- 4 Respostas
- 2991 Exibições
- Última mensagem por Molina

Sex Mar 06, 2009 12:47
Funções
-
- Questao de Funçao
por leilahomsi » Qua Jan 09, 2013 19:19
- 1 Respostas
- 1312 Exibições
- Última mensagem por e8group

Qua Jan 09, 2013 22:38
Funções
-
- [Questão de Função]
por zanotto » Sex Mar 21, 2014 23:18
- 3 Respostas
- 2225 Exibições
- Última mensagem por Russman

Sáb Mar 22, 2014 01:22
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


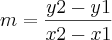





 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.