 por Claudin » Sáb Mai 21, 2011 16:17
por Claudin » Sáb Mai 21, 2011 16:17
Consegui chegar em um resultado mas nao sei se é o correto
se for possívvel algm poderia postar a operação discriminando passo a passo! Obrigado
![\lim_{x\rightarrow-\infty}\frac{(x^7-4x^5-12x^4+8x^3-2x^2)^5}{\sqrt[4]{(x^8-14x^5+13x^4-3x^6)^{36}}} \lim_{x\rightarrow-\infty}\frac{(x^7-4x^5-12x^4+8x^3-2x^2)^5}{\sqrt[4]{(x^8-14x^5+13x^4-3x^6)^{36}}}](/latexrender/pictures/5377cd97945c9021565fcfb41aea1754.png)
Acabei encontrando

Abraço
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por FilipeCaceres » Seg Mai 23, 2011 20:53
por FilipeCaceres » Seg Mai 23, 2011 20:53
Por que você não posta sua solução, assim é possível ver onde você esta errado e lhe mostrar o que você precisa estudar.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Claudin » Seg Mai 23, 2011 21:02
por Claudin » Seg Mai 23, 2011 21:02
Calculando através dos expoentes de maior valor encontrei:
![\lim_{x\rightarrow-\infty}\frac{x^{35}}{\sqrt[4]{x^{288}}} = -\infty \lim_{x\rightarrow-\infty}\frac{x^{35}}{\sqrt[4]{x^{288}}} = -\infty](/latexrender/pictures/5a984c4d0fc2599e0d024c9c152b0db8.png)
Felipe dps poderia me ajudar em outros topicos
viewtopic.php?f=120&t=4872obrigado.
Editado pela última vez por
Claudin em Seg Mai 23, 2011 22:07, em um total de 1 vez.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por FilipeCaceres » Seg Mai 23, 2011 22:01
por FilipeCaceres » Seg Mai 23, 2011 22:01
Fazendo conforme você disse, com os maoires expoente temos,
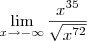
Como x<0 temos,
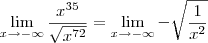
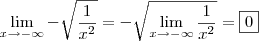
Espero que seja isso.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Claudin » Seg Mai 23, 2011 22:09
por Claudin » Seg Mai 23, 2011 22:09
corrigi minha resolução
era pra ter escrito desse modo ai em cima
mas n intendi esse seu
![\sqrt[]{x^{72}} \sqrt[]{x^{72}}](/latexrender/pictures/cd5ee38781cb2be9845dab9dd947465e.png)
como vc transformou raiz quarta em raiz quadrada?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por FilipeCaceres » Seg Mai 23, 2011 22:17
por FilipeCaceres » Seg Mai 23, 2011 22:17
Fiz o seguinte,
![\sqrt[\frac{4}{4}]{x^{\frac{288}{4}}}}=\sqrt{x^{72}} \sqrt[\frac{4}{4}]{x^{\frac{288}{4}}}}=\sqrt{x^{72}}](/latexrender/pictures/04881454186ef3e13222f2143b2c7e53.png)
Entendeu?
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Claudin » Seg Mai 23, 2011 22:22
por Claudin » Seg Mai 23, 2011 22:22
Vc tirou da raiz quarta e dividiu 288 por 4 ate ai entendi
porem essa operaçao que resultou em -
![\frac{1}{\sqrt[]{x^2}} \frac{1}{\sqrt[]{x^2}}](/latexrender/pictures/e60bdbcf6d85ae4f602c4496fb7d46e3.png)
nao compreendi!
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por FilipeCaceres » Seg Mai 23, 2011 22:36
por FilipeCaceres » Seg Mai 23, 2011 22:36
Você precisa saber que:
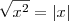
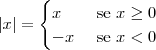
Como

, significa que
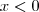
Assim temos

Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Claudin » Seg Mai 23, 2011 22:40
por Claudin » Seg Mai 23, 2011 22:40
Compreendi sim Felipe
Obrigado pela explicação.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Ter Mai 24, 2011 14:48
por Claudin » Ter Mai 24, 2011 14:48
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Ter Mai 24, 2011 17:51
por LuizAquino » Ter Mai 24, 2011 17:51
Mensagem corrigida pelo usuário
norberto.
Editado pela última vez por
LuizAquino em Ter Mai 24, 2011 18:30, em um total de 1 vez.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por norberto » Ter Mai 24, 2011 18:15
por norberto » Ter Mai 24, 2011 18:15
Ok. Só foi cometido um pequeno engano.
![\sqrt[\frac{4}_{4}]{x^{\frac{288}_{4}}} = x^{72} \sqrt[\frac{4}_{4}]{x^{\frac{288}_{4}}} = x^{72}](/latexrender/pictures/c2463ffd962fa83aa9eb7f587e4df3dc.png)
Abraços.
-
norberto
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Qua Mai 18, 2011 04:38
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Claudin » Ter Mai 24, 2011 20:50
por Claudin » Ter Mai 24, 2011 20:50
Então pensei corretamente
só esqueci de fazer a conversão de
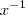
EM

"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por FilipeCaceres » Ter Mai 24, 2011 21:15
por FilipeCaceres » Ter Mai 24, 2011 21:15
Muito lamentável o que eu fiz, ainda por cima te expliquei

Abraço Claudin.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Claudin » Qua Mai 25, 2011 17:25
por Claudin » Qua Mai 25, 2011 17:25
ao retirar o índice 4 da raiz quarta logicamente retira a raiz
então não ficaria assim não?
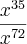
como ficaria a resposta final
analisei novamente e vi que nao ficaria como eu pensei e sim
como postei aqui agora!
qual seria o resultado entao?
Abraço
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Qui Mai 26, 2011 13:49
por LuizAquino » Qui Mai 26, 2011 13:49
Que tal revisar as propriedades de potenciação?
Se
a é não nulo, então
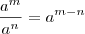
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Qui Mai 26, 2011 14:57
por Claudin » Qui Mai 26, 2011 14:57
LuizAquino escreveu:Que tal revisar as propriedades de potenciação?
Se
a é não nulo, então
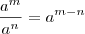
.
Você não está entendendo minha dúvida Luiz.
Essa propriedade pelo qual escreveu aqui em cima é básica e logicamente eu sei.
Eu perguntei, pois eu tinha dito ai em cima
que eu pensei assim
![\frac{x^{35}}{\sqrt[4]{x^{288}}} = \frac{x^{35}}{\sqrt[]{x^{72}}} \frac{x^{35}}{\sqrt[4]{x^{288}}} = \frac{x^{35}}{\sqrt[]{x^{72}}}](/latexrender/pictures/7655c3f6c9da9c73e97c49158a9f5cbc.png)
=
![\frac{x^{35}}{\sqrt[]{(x^{36})^2}} = \frac{x^{35}}{x^{36}} \frac{x^{35}}{\sqrt[]{(x^{36})^2}} = \frac{x^{35}}{x^{36}}](/latexrender/pictures/9d2fc5fd481fa4eff51181b959249af4.png)
=

Porém, eu percebi que dividindo o expoente 288 por 4, a raiz que até o momento era de índice 4 seria anulada
pela propriedade de radiciação.
![\sqrt[n]{a^x} = \sqrt[n]{a^\frac{x}{n}} = a^\frac{x}{n} \sqrt[n]{a^x} = \sqrt[n]{a^\frac{x}{n}} = a^\frac{x}{n}](/latexrender/pictures/a3f070f15c88ff129a8c6e77a596cdfd.png)
Estou correto?
Entao no caso ficaria isso aqui?
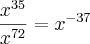
Obrigado
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Qui Mai 26, 2011 15:24
por LuizAquino » Qui Mai 26, 2011 15:24
Correção:
![\sqrt[n]{a^x} = \sqrt[\frac{n}{n}]{a^\frac{x}{n}} = a^\frac{x}{n} \sqrt[n]{a^x} = \sqrt[\frac{n}{n}]{a^\frac{x}{n}} = a^\frac{x}{n}](/latexrender/pictures/3ed1cf1750e1a59be1a3cc098f3edb54.png)
.
Vale lembrar que se
n for par deve-se ter cuidado com o fato de que
a deve ser positivo.
Você não está entendendo minha dúvida Luiz.
Essa propriedade pelo qual escreveu aqui em cima é básica e logicamente eu sei.
Se você sabia da propriedade, então bastava ter usado.
Entao no caso ficaria isso aqui?
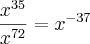
Sim.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Qui Mai 26, 2011 15:32
por Claudin » Qui Mai 26, 2011 15:32
"Vale lembrar que se n for par deve-se ter cuidado com o fato de que a deve ser positivo."
Claro, raiz de índice par só aceita números positivos. E raiz de índice ímpar pode aceitar números negativos!
"Se você sabia da propriedade, então bastava ter usado."
Só não utilizei a propriedade pois na resolução anterior que eu fiz errada
eu nao tinha sido corrigido, então não sabia se a resposta era mesmo essa que eu resolvi agora!
Mas que bom que tudo foi esclarecido!
Obrigado
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limite] Dúvida limite com raizes
por rqaugusto » Dom Abr 30, 2017 23:23
- 0 Respostas
- 3115 Exibições
- Última mensagem por rqaugusto

Dom Abr 30, 2017 23:23
Cálculo: Limites, Derivadas e Integrais
-
- Limite - Duvida
por Claudin » Qua Mai 18, 2011 18:32
- 3 Respostas
- 2594 Exibições
- Última mensagem por Claudin

Qua Mai 18, 2011 20:45
Cálculo: Limites, Derivadas e Integrais
-
- Duvida - Limite
por Claudin » Qua Mai 18, 2011 21:19
- 6 Respostas
- 3302 Exibições
- Última mensagem por Claudin

Qui Mai 19, 2011 12:31
Cálculo: Limites, Derivadas e Integrais
-
- Duvida - Limite
por Claudin » Qui Mai 19, 2011 09:20
- 5 Respostas
- 3070 Exibições
- Última mensagem por Claudin

Dom Mai 22, 2011 16:19
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] duvida
por beel » Sáb Set 03, 2011 20:32
- 4 Respostas
- 1937 Exibições
- Última mensagem por beel

Dom Set 04, 2011 15:30
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow-\infty}\frac{(x^7-4x^5-12x^4+8x^3-2x^2)^5}{\sqrt[4]{(x^8-14x^5+13x^4-3x^6)^{36}}} \lim_{x\rightarrow-\infty}\frac{(x^7-4x^5-12x^4+8x^3-2x^2)^5}{\sqrt[4]{(x^8-14x^5+13x^4-3x^6)^{36}}}](/latexrender/pictures/5377cd97945c9021565fcfb41aea1754.png)


![\lim_{x\rightarrow-\infty}\frac{(x^7-4x^5-12x^4+8x^3-2x^2)^5}{\sqrt[4]{(x^8-14x^5+13x^4-3x^6)^{36}}} \lim_{x\rightarrow-\infty}\frac{(x^7-4x^5-12x^4+8x^3-2x^2)^5}{\sqrt[4]{(x^8-14x^5+13x^4-3x^6)^{36}}}](/latexrender/pictures/5377cd97945c9021565fcfb41aea1754.png)



![\lim_{x\rightarrow-\infty}\frac{x^{35}}{\sqrt[4]{x^{288}}} = -\infty \lim_{x\rightarrow-\infty}\frac{x^{35}}{\sqrt[4]{x^{288}}} = -\infty](/latexrender/pictures/5a984c4d0fc2599e0d024c9c152b0db8.png)

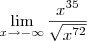
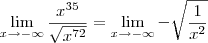
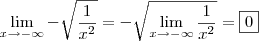

![\sqrt[]{x^{72}} \sqrt[]{x^{72}}](/latexrender/pictures/cd5ee38781cb2be9845dab9dd947465e.png)

![\sqrt[\frac{4}{4}]{x^{\frac{288}{4}}}}=\sqrt{x^{72}} \sqrt[\frac{4}{4}]{x^{\frac{288}{4}}}}=\sqrt{x^{72}}](/latexrender/pictures/04881454186ef3e13222f2143b2c7e53.png)

![\frac{1}{\sqrt[]{x^2}} \frac{1}{\sqrt[]{x^2}}](/latexrender/pictures/e60bdbcf6d85ae4f602c4496fb7d46e3.png)

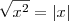
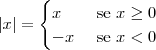
 , significa que
, significa que 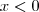



![\lim_{x\rightarrow-\infty}\frac{x^{35}}{\sqrt[2]{(x^{36})^2}} \lim_{x\rightarrow-\infty}\frac{x^{35}}{\sqrt[2]{(x^{36})^2}}](/latexrender/pictures/3bd476081ad3ffb4d847be39d4b2cf6f.png)
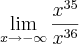
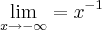


![\sqrt[\frac{4}_{4}]{x^{\frac{288}_{4}}} = x^{72} \sqrt[\frac{4}_{4}]{x^{\frac{288}_{4}}} = x^{72}](/latexrender/pictures/c2463ffd962fa83aa9eb7f587e4df3dc.png)

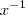 EM
EM 



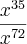

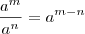 .
.
.
![\frac{x^{35}}{\sqrt[4]{x^{288}}} = \frac{x^{35}}{\sqrt[]{x^{72}}} \frac{x^{35}}{\sqrt[4]{x^{288}}} = \frac{x^{35}}{\sqrt[]{x^{72}}}](/latexrender/pictures/7655c3f6c9da9c73e97c49158a9f5cbc.png) =
= ![\frac{x^{35}}{\sqrt[]{(x^{36})^2}} = \frac{x^{35}}{x^{36}} \frac{x^{35}}{\sqrt[]{(x^{36})^2}} = \frac{x^{35}}{x^{36}}](/latexrender/pictures/9d2fc5fd481fa4eff51181b959249af4.png) =
= 
![\sqrt[n]{a^x} = \sqrt[n]{a^\frac{x}{n}} = a^\frac{x}{n} \sqrt[n]{a^x} = \sqrt[n]{a^\frac{x}{n}} = a^\frac{x}{n}](/latexrender/pictures/a3f070f15c88ff129a8c6e77a596cdfd.png)
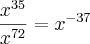

![\sqrt[n]{a^x} = \sqrt[\frac{n}{n}]{a^\frac{x}{n}} = a^\frac{x}{n} \sqrt[n]{a^x} = \sqrt[\frac{n}{n}]{a^\frac{x}{n}} = a^\frac{x}{n}](/latexrender/pictures/3ed1cf1750e1a59be1a3cc098f3edb54.png) .
.

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.