-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 477696 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 528434 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 492002 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 696121 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2104425 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por ewald » Qui Mai 05, 2011 19:08
por ewald » Qui Mai 05, 2011 19:08
![\lim_{x\rightarrow 1} \frac{\sqrt[2]{x} -{x}^{2}}{1 -\sqrt[2]{x}} \lim_{x\rightarrow 1} \frac{\sqrt[2]{x} -{x}^{2}}{1 -\sqrt[2]{x}}](/latexrender/pictures/a918e1d271960315037b9918c635538e.png)
Oi preciso de uma forma de se resolver este limite SEM o uso de L'hopital. Agradeço tmb se puderem deixar alguns dos 'macetes' para extrair a indeterminaçao de limites.
Caso LCMAquino esteja lendo : Gostei muito das tuas aulas no youtube, no entanto nao achei alguma que se dedique a mostrar metodos de extraçao da indeterminaçao do limite em questoes mais elaboradas, que sem duvidas é a parte de limites que mais causa duvidas (pra mim essa que eu botei ja é elaborada! ¬¬' ).
Obs.: desculpa os erros de portugues!
-
ewald
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Qui Mai 05, 2011 17:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Eletrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite indeterminado
por ewald » Qui Mai 05, 2011 17:55
- 1 Respostas
- 1582 Exibições
- Última mensagem por LuizAquino

Qui Mai 05, 2011 18:12
Cálculo: Limites, Derivadas e Integrais
-
- Limite indeterminado
por ewald » Ter Mai 17, 2011 15:40
- 13 Respostas
- 5651 Exibições
- Última mensagem por FilipeCaceres

Qua Mai 18, 2011 15:47
Cálculo: Limites, Derivadas e Integrais
-
- Limite indeterminado ? - ?
por cjunior94 » Ter Mai 01, 2012 22:00
- 1 Respostas
- 1423 Exibições
- Última mensagem por LuizAquino

Qua Mai 02, 2012 14:17
Cálculo: Limites, Derivadas e Integrais
-
- Duvida limite indeterminado
por ewald » Seg Mai 09, 2011 17:20
- 1 Respostas
- 2299 Exibições
- Última mensagem por LuizAquino

Seg Mai 09, 2011 20:01
Cálculo: Limites, Derivadas e Integrais
-
- Limite trigonometrico indeterminado
por ewald » Qui Mai 26, 2011 15:15
- 11 Respostas
- 4907 Exibições
- Última mensagem por MarceloFantini

Dom Mai 29, 2011 02:32
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 19 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow 1} \frac{\sqrt[2]{x} -{x}^{2}}{1 -\sqrt[2]{x}} \lim_{x\rightarrow 1} \frac{\sqrt[2]{x} -{x}^{2}}{1 -\sqrt[2]{x}}](/latexrender/pictures/a918e1d271960315037b9918c635538e.png)


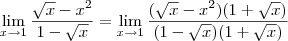
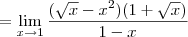
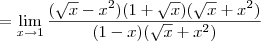
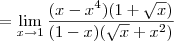
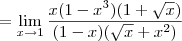
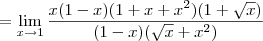
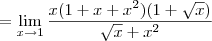
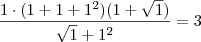



 .
.



