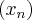 uma sequencia de números reais.
uma sequencia de números reais.a) Desmontre que
 se e somente se
se e somente se 
b) Vale um resultado geral da forma "
 se e somente se
se e somente se 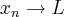
c) Seja
![a\in(-1,0] a\in(-1,0]](/latexrender/pictures/1a7c573ab1fc4b974fc3211c9c28405a.png) . Mostre que
. Mostre que 
Preciso muito desta ajuda
Obrigado

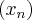 uma sequencia de números reais.
uma sequencia de números reais. se e somente se
se e somente se 
 se e somente se
se e somente se 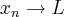
![a\in(-1,0] a\in(-1,0]](/latexrender/pictures/1a7c573ab1fc4b974fc3211c9c28405a.png) . Mostre que
. Mostre que 

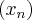 uma sequencia de números reais.
uma sequencia de números reais. se e somente se
se e somente se 
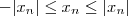 e lembre-se do Teorema do Confronto.
e lembre-se do Teorema do Confronto.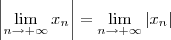 .
. se e somente se
se e somente se 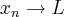
![a\in(-1,0] a\in(-1,0]](/latexrender/pictures/1a7c573ab1fc4b974fc3211c9c28405a.png) . Mostre que
. Mostre que  .
.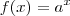 com
com 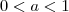 é decrescente. Além disso, temos que
é decrescente. Além disso, temos que  .
.
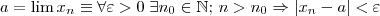 ?
?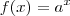 com
com 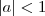 é decrescente? Ele não pode usar o limite que você mencionou pois justamente o que ele quer é mostrar que o limite da sequência é zero. Como não sabemos, eu diria que talvez ele tenha que provar que
é decrescente? Ele não pode usar o limite que você mencionou pois justamente o que ele quer é mostrar que o limite da sequência é zero. Como não sabemos, eu diria que talvez ele tenha que provar que  é decrescente e depois mostrar que o limite é zero.
é decrescente e depois mostrar que o limite é zero.







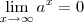 , pois é o que queremos provar.
, pois é o que queremos provar.

 será crescente e converge para zero
será crescente e converge para zero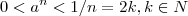 será decrescence e converge para zero
será decrescence e converge para zero
 exista
exista  natural tal que
natural tal que 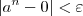 sempre que
sempre que  .
.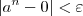

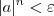
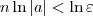
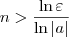
 basta tomar qualquer
basta tomar qualquer  maior ou igual a
maior ou igual a 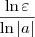 .
.
 natural tal que
natural tal que 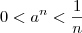 para
para  . Aplicando teorema do confronto,
. Aplicando teorema do confronto,  e
e  , logo
, logo 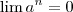 .
.

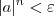 e queremos isolar a variável n. Para fazer isso vamos precisar usar o conceito de logaritmos.
e queremos isolar a variável n. Para fazer isso vamos precisar usar o conceito de logaritmos.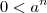 como você escreveu. Por mais que você tome n maior do que um certo
como você escreveu. Por mais que você tome n maior do que um certo  , haverá valores para os quais
, haverá valores para os quais  . Portanto, não se pode aplicar o Teorema do Confronto da maneira como você sugeriu.
. Portanto, não se pode aplicar o Teorema do Confronto da maneira como você sugeriu.
 natural tal que
natural tal que 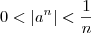 para
para  . Assim, aplicando confronto, temos que
. Assim, aplicando confronto, temos que 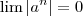 , logo
, logo 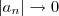 . Falta provar que
. Falta provar que  . Note que
. Note que 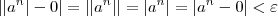 . Assim, pela definição de limite temos que
. Assim, pela definição de limite temos que  .
.

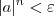 e queremos isolar a variável n não há problema em usar os conceitos de logaritmos nesse exercício. Pelo que percebo, não vamos chegar a um consenso quanto a isso, portanto acho o mais prudente cada um respeitar a opinião do outro.
e queremos isolar a variável n não há problema em usar os conceitos de logaritmos nesse exercício. Pelo que percebo, não vamos chegar a um consenso quanto a isso, portanto acho o mais prudente cada um respeitar a opinião do outro. . De qualquer modo, isso não chega a ser tão problemático, pois tomando a=0 a prova é trivial. Em seguida, bastava tomar a no intervalo (-1, 0) e continuar a solução como descrito.
. De qualquer modo, isso não chega a ser tão problemático, pois tomando a=0 a prova é trivial. Em seguida, bastava tomar a no intervalo (-1, 0) e continuar a solução como descrito. que atenda
que atenda 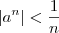 , com
, com 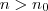 . Isso não segue assim tão direto.
. Isso não segue assim tão direto. é o mesmo que
é o mesmo que 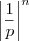 , para algum p > 1. Como para números n muito grandes,
, para algum p > 1. Como para números n muito grandes, 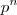 será maior do que n, então teremos que
será maior do que n, então teremos que 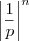 será menor do que
será menor do que  .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes

 .
.
 :
: