 por maykonnunes » Qua Abr 27, 2011 09:54
por maykonnunes » Qua Abr 27, 2011 09:54
Seja
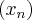
uma sequencia de números reais.
a) Desmontre que

se e somente se

b) Vale um resultado geral da forma "

se e somente se
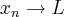
c) Seja
![a\in(-1,0] a\in(-1,0]](/latexrender/pictures/1a7c573ab1fc4b974fc3211c9c28405a.png)
. Mostre que

Preciso muito desta ajuda
Obrigado
-
maykonnunes
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 02:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por LuizAquino » Qui Abr 28, 2011 23:07
por LuizAquino » Qui Abr 28, 2011 23:07
Seja
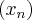
uma sequencia de números reais.
a) Desmontre que

se e somente se

Note que
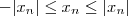
e lembre-se do
Teorema do Confronto.
Além disso, lembre-se que
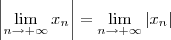
.
b) Vale um resultado geral da forma:

se e somente se
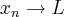
Considere o lembrete dado em a)
c) Seja
![a\in(-1,0] a\in(-1,0]](/latexrender/pictures/1a7c573ab1fc4b974fc3211c9c28405a.png)
. Mostre que

.
Lembre-se que a função
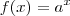
com
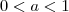
é decrescente. Além disso, temos que

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por MarceloFantini » Sex Abr 29, 2011 00:05
por MarceloFantini » Sex Abr 29, 2011 00:05
Será que talvez ele não tenha que demonstrar pela definição?
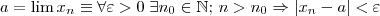
?
No caso do item c, será que já é dado que a função
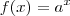
com
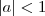
é decrescente? Ele não pode usar o limite que você mencionou pois justamente o que ele quer é mostrar que o limite da sequência é zero. Como não sabemos, eu diria que talvez ele tenha que provar que

é decrescente e depois mostrar que o limite é zero.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Sex Abr 29, 2011 00:19
por LuizAquino » Sex Abr 29, 2011 00:19
Isso tudo depende da ordem adotada no curso.
De modo geral, primeiro estudamos as funções exponenciais e seus limites antes de falar de sequências.
É óbvio que se esse estudo não foi feito antes, então não podemos utilizá-lo na demonstração em questão.
De qualquer maneira, as demonstrações são análogas, portanto uma pode inspirar a outra. Eis o motivo da dica que dei.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por MarceloFantini » Sex Abr 29, 2011 00:25
por MarceloFantini » Sex Abr 29, 2011 00:25
No livro do Elon, Análise Real Vol. 1, não é feito assim. Não faz sentido falar em limite de função quando não se definiu ainda limite de sequência, pois se define limites de funções como limites de sequências de números num intervalo tal que a função aplicada na sequência convirja para o número desejado.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por maykonnunes » Sex Abr 29, 2011 00:40
por maykonnunes » Sex Abr 29, 2011 00:40
so que tem algo ela vai ser crescente de -1 para 0 não é??
-
maykonnunes
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 02:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por MarceloFantini » Sex Abr 29, 2011 00:42
por MarceloFantini » Sex Abr 29, 2011 00:42
O que será crescente?
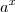
com

?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Sex Abr 29, 2011 01:01
por LuizAquino » Sex Abr 29, 2011 01:01
Prezado Fantini,
Até certo ponto, a ordem dos assuntos é uma questão de estilo de cada autor. Obviamente, o Elon Lages não é o único autor existente.
Há livros que começam com limites de funções para em seguida enxergar o limite de sequências como um caso discreto do limite de funções. Ou seja, toma-se uma função f(x) e enxerga-se a sequência como an = f(n), com n natural. Essa ordem dos conteúdos, por exemplo, é muito comum em livros de Cálculo.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por MarceloFantini » Sex Abr 29, 2011 13:14
por MarceloFantini » Sex Abr 29, 2011 13:14
Com todo respeito Luiz, uma sequência é enxergada como uma função sim, mas o objetivo de um curso de Análise é construir os conhecimentos de Cálculo rigorosamente, e portanto construir o conceito de limite de uma função contínua partindo de casos discretos como sequência. Logo, reitero que não se pode usar que
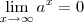
, pois é o que queremos provar.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por maykonnunes » Sex Abr 29, 2011 15:11
por maykonnunes » Sex Abr 29, 2011 15:11
acho que a ideia é a seguinte como intervalo (-1,0] que se divide em duas
>

será crescente e converge para zero
>
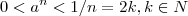
será decrescence e converge para zero
Ainda não poço falar em função apenas en sequência
Abraços
-
maykonnunes
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 02:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por LuizAquino » Sex Abr 29, 2011 17:45
por LuizAquino » Sex Abr 29, 2011 17:45
Tudo bem, já que a ideia é não usar funções, então vejamos uma solução.
Para
a=0, a prova é trivial.
Suponha que
a esteja no intervalo (-1, 0).
Queremos que para todo

exista

natural tal que
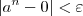
sempre que

.
Desenvolvendo a primeira inequação, obtemos que:
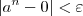

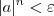
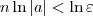
Como |
a| está no intervalo (0, 1), temos que ln|
a| < 0. Portanto, multiplicando toda a inequação por 1/ln|
a| devemos trocar o seu sentido.
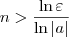
Logo, dado

basta tomar qualquer

maior ou igual a
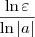
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por MarceloFantini » Sáb Abr 30, 2011 02:35
por MarceloFantini » Sáb Abr 30, 2011 02:35
Luiz, perceba que você é contraditório em sua mensagem. Primeiro, diz não usar funções, e depois usa logaritmo natural.
Acredito que um jeito de resolver essa questão seja dizer que existe

natural tal que
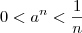
para

. Aplicando teorema do confronto,

e

, logo
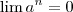
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Sáb Abr 30, 2011 08:36
por LuizAquino » Sáb Abr 30, 2011 08:36
Não há problema algum em aplicar ln em ambos os lados da inequação. Note que temos a inequação
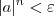
e queremos isolar a variável
n. Para fazer isso vamos precisar usar o conceito de logaritmos.
Quando disse "não usar funções" quis dizer que não usaria o conhecimento sobre as funções exponenciais como eu havia sugerido antes. Eu imaginei que isso ficaria claro considerando as mensagens anteriores, mas vejo que eu deveria ter sido mais específico. Desculpe-me por isso.
Além disso, note que
a está no intervalo (-1, 0]. Desse modo, nem sempre é válido que
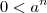
como você escreveu. Por mais que você tome
n maior do que um certo

, haverá valores para os quais

. Portanto, não se pode aplicar o Teorema do Confronto da maneira como você sugeriu.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por MarceloFantini » Sáb Abr 30, 2011 16:25
por MarceloFantini » Sáb Abr 30, 2011 16:25
Aquino, acredito que ambos não fomos claros. Concordo que minha demonstração fora incompleta e arrumarei a seguir. Entretanto, preciso reforçar que o seu uso de logaritmo
não é correto. Quando eu disse não usar funções, eu digo não usar funções elementares tradicionais, como seno, cosseno, logaritmo, exponencial, etc.
Consertando, basta afirmar que existe

natural tal que
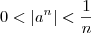
para

. Assim, aplicando confronto, temos que
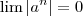
, logo
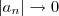
. Falta provar que

. Note que
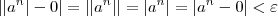
. Assim, pela definição de limite temos que

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Sáb Abr 30, 2011 16:51
por LuizAquino » Sáb Abr 30, 2011 16:51
Eu volto a afirmar que se temos a inequação
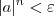
e queremos isolar a variável
n não há problema em usar os conceitos de logaritmos nesse exercício. Pelo que percebo, não vamos chegar a um consenso quanto a isso, portanto acho o mais prudente cada um respeitar a opinião do outro.
Quanto a sua solução, falta ter o cuidado de tomar
a não nulo, haja vista que como
a está no intervalo (-1, 0], se tomarmos
a=0 não ocorrerá que

. De qualquer modo, isso não chega a ser tão problemático, pois tomando
a=0 a prova é trivial. Em seguida, bastava tomar
a no intervalo (-1, 0) e continuar a solução como descrito.
Além disso, falta justificar por que é possível afirmar que existe

que atenda
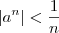
, com
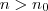
. Isso não segue assim tão direto.
Uma alternativa seria perceber que como 0 < |
a| < 1, então

é o mesmo que
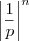
, para algum
p > 1. Como para números
n muito grandes,
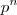
será maior do que
n, então teremos que
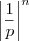
será menor do que

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [sequencia] Calcular limite de sequencia por definição
 por amigao » Ter Abr 15, 2014 15:15
por amigao » Ter Abr 15, 2014 15:15
- 4 Respostas
- 4003 Exibições
- Última mensagem por e8group

Dom Mai 11, 2014 17:09
Sequências
-
- Sequencia
por Amparo » Dom Mar 09, 2008 16:26
- 3 Respostas
- 3597 Exibições
- Última mensagem por nietzsche

Sex Set 02, 2011 00:42
Sequências
-
- Sequencia
por Abner » Qua Jan 26, 2011 19:15
- 1 Respostas
- 2410 Exibições
- Última mensagem por Neperiano

Qua Ago 31, 2011 18:43
Geometria Plana
-
- [Sequência]
por elizangelasss20 » Qua Abr 11, 2012 19:12
- 4 Respostas
- 2900 Exibições
- Última mensagem por elizangelasss20

Qua Abr 11, 2012 20:52
Sequências
-
- Sequência
por GrazielaSilva » Qui Nov 01, 2012 10:20
- 1 Respostas
- 3929 Exibições
- Última mensagem por young_jedi

Qui Nov 01, 2012 13:49
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
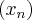 uma sequencia de números reais.
uma sequencia de números reais. se e somente se
se e somente se 
 se e somente se
se e somente se 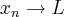
![a\in(-1,0] a\in(-1,0]](/latexrender/pictures/1a7c573ab1fc4b974fc3211c9c28405a.png) . Mostre que
. Mostre que 

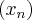 uma sequencia de números reais.
uma sequencia de números reais. se e somente se
se e somente se 
 se e somente se
se e somente se 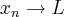
![a\in(-1,0] a\in(-1,0]](/latexrender/pictures/1a7c573ab1fc4b974fc3211c9c28405a.png) . Mostre que
. Mostre que 

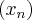 uma sequencia de números reais.
uma sequencia de números reais. se e somente se
se e somente se 
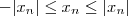 e lembre-se do Teorema do Confronto.
e lembre-se do Teorema do Confronto.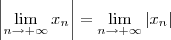 .
. se e somente se
se e somente se 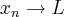
![a\in(-1,0] a\in(-1,0]](/latexrender/pictures/1a7c573ab1fc4b974fc3211c9c28405a.png) . Mostre que
. Mostre que  .
.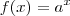 com
com 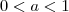 é decrescente. Além disso, temos que
é decrescente. Além disso, temos que  .
.
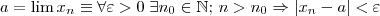 ?
?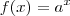 com
com 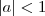 é decrescente? Ele não pode usar o limite que você mencionou pois justamente o que ele quer é mostrar que o limite da sequência é zero. Como não sabemos, eu diria que talvez ele tenha que provar que
é decrescente? Ele não pode usar o limite que você mencionou pois justamente o que ele quer é mostrar que o limite da sequência é zero. Como não sabemos, eu diria que talvez ele tenha que provar que  é decrescente e depois mostrar que o limite é zero.
é decrescente e depois mostrar que o limite é zero.







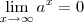 , pois é o que queremos provar.
, pois é o que queremos provar.

 será crescente e converge para zero
será crescente e converge para zero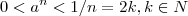 será decrescence e converge para zero
será decrescence e converge para zero
 exista
exista  natural tal que
natural tal que 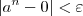 sempre que
sempre que  .
.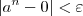

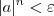
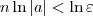
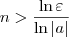
 basta tomar qualquer
basta tomar qualquer  maior ou igual a
maior ou igual a 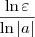 .
.
 natural tal que
natural tal que 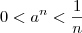 para
para  . Aplicando teorema do confronto,
. Aplicando teorema do confronto,  e
e  , logo
, logo 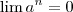 .
.

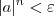 e queremos isolar a variável n. Para fazer isso vamos precisar usar o conceito de logaritmos.
e queremos isolar a variável n. Para fazer isso vamos precisar usar o conceito de logaritmos.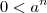 como você escreveu. Por mais que você tome n maior do que um certo
como você escreveu. Por mais que você tome n maior do que um certo  , haverá valores para os quais
, haverá valores para os quais  . Portanto, não se pode aplicar o Teorema do Confronto da maneira como você sugeriu.
. Portanto, não se pode aplicar o Teorema do Confronto da maneira como você sugeriu.
 natural tal que
natural tal que 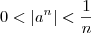 para
para  . Assim, aplicando confronto, temos que
. Assim, aplicando confronto, temos que 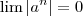 , logo
, logo 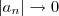 . Falta provar que
. Falta provar que  . Note que
. Note que 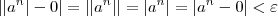 . Assim, pela definição de limite temos que
. Assim, pela definição de limite temos que  .
.

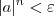 e queremos isolar a variável n não há problema em usar os conceitos de logaritmos nesse exercício. Pelo que percebo, não vamos chegar a um consenso quanto a isso, portanto acho o mais prudente cada um respeitar a opinião do outro.
e queremos isolar a variável n não há problema em usar os conceitos de logaritmos nesse exercício. Pelo que percebo, não vamos chegar a um consenso quanto a isso, portanto acho o mais prudente cada um respeitar a opinião do outro. . De qualquer modo, isso não chega a ser tão problemático, pois tomando a=0 a prova é trivial. Em seguida, bastava tomar a no intervalo (-1, 0) e continuar a solução como descrito.
. De qualquer modo, isso não chega a ser tão problemático, pois tomando a=0 a prova é trivial. Em seguida, bastava tomar a no intervalo (-1, 0) e continuar a solução como descrito. que atenda
que atenda 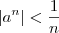 , com
, com 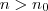 . Isso não segue assim tão direto.
. Isso não segue assim tão direto. é o mesmo que
é o mesmo que 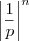 , para algum p > 1. Como para números n muito grandes,
, para algum p > 1. Como para números n muito grandes, 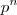 será maior do que n, então teremos que
será maior do que n, então teremos que 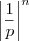 será menor do que
será menor do que  .
.