 por leka figuer » Qua Abr 27, 2011 15:06
por leka figuer » Qua Abr 27, 2011 15:06
Não sei se respondi certo a um dos exercícios que estou tentando resolver
Dados os conjuntos A= {1,5,9}, B={7,8,9} e C= {1,5} efetuar: A

B

C
Eu respondi que seriam conjuntos disjuntos, uma vez que os conjuntos B e C não conteem os mesmos elementos
Se errei por favor me ajudem explicando o porquê. Obrigada
-
leka figuer
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Abr 21, 2011 16:16
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Abelardo » Qua Abr 27, 2011 19:20
por Abelardo » Qua Abr 27, 2011 19:20
Se existir algum elemento em

, significa que ele
pertence também a A, B e C. Lembra-se de como chamamos o conjunto ''solução'' da intersecção de três conjuntos disjuntos?
Editado pela última vez por
Abelardo em Qui Abr 28, 2011 01:21, em um total de 1 vez.
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Qua Abr 27, 2011 19:52
por MarceloFantini » Qua Abr 27, 2011 19:52
Abelardo, você consegue exibir um elemento que esteja nos três conjuntos ao mesmo tempo?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por leka figuer » Qua Abr 27, 2011 20:34
por leka figuer » Qua Abr 27, 2011 20:34
Ainda estou um pouco na dúvida... como não há um elemento em comum nos três conjuntos ao mesmo tempo, então,

ou seja conjunto disjunto, seria a resposta adequada a nivel de ensino fundamental e médio ?
-
leka figuer
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Abr 21, 2011 16:16
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Qua Abr 27, 2011 20:50
por MarceloFantini » Qua Abr 27, 2011 20:50
Você quer dizer
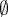
, o
conjunto vazio. E sim, a intersecção dos três conjuntos é vazia. Note que
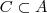
, onde C é um conjunto tomado especialmente para que fosse disjunto a B.
Editado pela última vez por
MarceloFantini em Qua Abr 27, 2011 21:27, em um total de 1 vez.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Abelardo » Qua Abr 27, 2011 21:13
por Abelardo » Qua Abr 27, 2011 21:13
Desculpe-me Fantini se o que escrevi não ficou claro. Eu tentei dar a dica ao ''leka figuer''... coloquei até ''Se existir algum''. Como ele mesmo observou, os conjuntos são disjuntos, logo a solução é ... (mania de professor do fundamental de falar quase tudo e deixar que os alunos completem a frase kkkk) o conjunto vazio.
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por leka figuer » Qui Abr 28, 2011 00:52
por leka figuer » Qui Abr 28, 2011 00:52
Uau! Agora entendi com muita clareza! Muito obrigada aos dois por promover a oportunidade de me aprofundar mais em matemática ( pois sou péssima em entender essa matéria rsrs) Abraços
-
leka figuer
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Abr 21, 2011 16:16
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Conjuntos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 B
B C
C
 B
B C
C
 , significa que ele pertence também a A, B e C. Lembra-se de como chamamos o conjunto ''solução'' da intersecção de três conjuntos disjuntos?
, significa que ele pertence também a A, B e C. Lembra-se de como chamamos o conjunto ''solução'' da intersecção de três conjuntos disjuntos?


 ou seja conjunto disjunto, seria a resposta adequada a nivel de ensino fundamental e médio ?
ou seja conjunto disjunto, seria a resposta adequada a nivel de ensino fundamental e médio ?
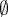 , o conjunto vazio. E sim, a intersecção dos três conjuntos é vazia. Note que
, o conjunto vazio. E sim, a intersecção dos três conjuntos é vazia. Note que 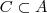 , onde C é um conjunto tomado especialmente para que fosse disjunto a B.
, onde C é um conjunto tomado especialmente para que fosse disjunto a B.


