 por Carolziiinhaaah » Qui Abr 21, 2011 16:19
por Carolziiinhaaah » Qui Abr 21, 2011 16:19
Se a equação do 2o grau ax^2 + bx + c = 0, a ? 0, admite as raízes reais não nulas x1 e x2, obter a equação de
raízes:

Uploaded with
ImageShack.us
-

Carolziiinhaaah
- Usuário Parceiro

-
- Mensagens: 77
- Registrado em: Sex Mai 28, 2010 14:12
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Qui Abr 21, 2011 16:30
por MarceloFantini » Qui Abr 21, 2011 16:30
Lembre-se da fatoração de polinômios:
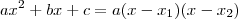
. Troque as raízes pelas que você tem e reescreva em termos dos coeficientes originais.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por SidneySantos » Qui Abr 21, 2011 17:01
por SidneySantos » Qui Abr 21, 2011 17:01
Editado pela última vez por
SidneySantos em Sex Abr 22, 2011 09:26, em um total de 2 vezes.
Um forte abraço e bom estudo!!!
-
SidneySantos
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Qua Abr 20, 2011 07:47
- Localização: Belém - Pará
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Educaçao Matemática
- Andamento: cursando
 por SidneySantos » Qui Abr 21, 2011 17:45
por SidneySantos » Qui Abr 21, 2011 17:45
Editado pela última vez por
SidneySantos em Sex Abr 22, 2011 09:28, em um total de 2 vezes.
Um forte abraço e bom estudo!!!
-
SidneySantos
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Qua Abr 20, 2011 07:47
- Localização: Belém - Pará
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Educaçao Matemática
- Andamento: cursando
 por SidneySantos » Qui Abr 21, 2011 17:56
por SidneySantos » Qui Abr 21, 2011 17:56
Um forte abraço e bom estudo!!!
-
SidneySantos
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Qua Abr 20, 2011 07:47
- Localização: Belém - Pará
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Educaçao Matemática
- Andamento: cursando
 por SidneySantos » Sex Abr 22, 2011 09:49
por SidneySantos » Sex Abr 22, 2011 09:49
Um forte abraço e bom estudo!!!
-
SidneySantos
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Qua Abr 20, 2011 07:47
- Localização: Belém - Pará
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Educaçao Matemática
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Soma e produto das raizes das equações.
por Thays » Ter Jan 22, 2013 12:41
- 3 Respostas
- 4163 Exibições
- Última mensagem por Thays

Qua Jan 23, 2013 10:11
Equações
-
- [raízes de números complexos] Raízes de uma equação com grau
por karenfreitas » Seg Ago 22, 2016 19:08
- 1 Respostas
- 8112 Exibições
- Última mensagem por adauto martins

Sáb Ago 27, 2016 16:11
Números Complexos
-
- [Radiciação] Raízes dentro de raízes
por mottasky » Ter Set 13, 2011 22:00
- 2 Respostas
- 2573 Exibições
- Última mensagem por mottasky

Qui Set 15, 2011 15:52
Álgebra Elementar
-
- Calculando a função através das coordenadas
por Fernanda Lauton » Dom Jun 13, 2010 20:36
- 2 Respostas
- 1627 Exibições
- Última mensagem por Fernanda Lauton

Seg Jun 14, 2010 16:06
Funções
-
- DETERMINAR FUNÇÃO ATRAVÉS DE COORDENADAS
por Fernanda Lauton » Qua Abr 06, 2011 14:41
- 1 Respostas
- 1733 Exibições
- Última mensagem por MarceloFantini

Qua Abr 06, 2011 19:24
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




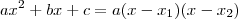 . Troque as raízes pelas que você tem e reescreva em termos dos coeficientes originais.
. Troque as raízes pelas que você tem e reescreva em termos dos coeficientes originais.




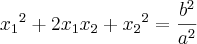
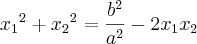

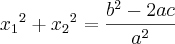
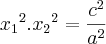

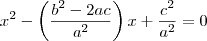
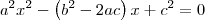




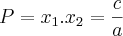
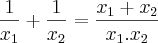









 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.