 por guillcn » Qua Abr 06, 2011 19:43
por guillcn » Qua Abr 06, 2011 19:43
O enunciado diz dado que x =
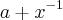
, a expressao

e igual a :
entao comecei a resoluçao

quando eu multipliquei o primeiro termo por

para
igualar as fracoes eu nao consegui dar prosseguimento ao exercicio. o que devo fazer ?
Grato desde ja.
Editado pela última vez por
guillcn em Qua Abr 06, 2011 20:37, em um total de 1 vez.
-
guillcn
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Ter Abr 05, 2011 16:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por guillcn » Qua Abr 06, 2011 20:39
por guillcn » Qua Abr 06, 2011 20:39
desculpe mas nao compreendi a logica da resolucao ou nao consegui relaciona-la com o exercicio porem obrigado pela ajuda e atençao.

-
guillcn
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Ter Abr 05, 2011 16:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Qua Abr 06, 2011 20:41
por MarceloFantini » Qua Abr 06, 2011 20:41
Caro Gui, refaça meus passos: passe
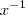
para o lado esquerdo da igualdade. Em seguida, eleve os dois ao quadrado, lembrando o produto notável
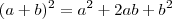
. Lembre-se também que
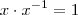
. Em seguida, isole
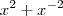
e veja que cairá onde eu cheguei. Refaça no papel que ficará mais claro.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por guillcn » Qua Abr 06, 2011 20:54
por guillcn » Qua Abr 06, 2011 20:54
Desculpe eu pensei q tinha q relacionar sua formula com a do exercicio.
Ok segui os passos e compreendi,muito obrigado .
Obs.no caso do
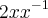
elimina-se o x pelo
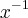
restando o +2.
Muito obrigado novamente.
-
guillcn
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Ter Abr 05, 2011 16:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Qua Abr 06, 2011 21:01
por MarceloFantini » Qua Abr 06, 2011 21:01
Só detalhando: sobra -2, mas quando volta para o lado direito fica +2, sim. Disponha, sempre que precisar crie um novo tópico para cada dúvida.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Trinomio Quadrado Perfeito (Complemento de quadrado)
por IgorFilipe » Qua Ago 17, 2011 23:01
- 2 Respostas
- 3760 Exibições
- Última mensagem por IgorFilipe

Qui Ago 18, 2011 15:52
Funções
-
- Quadrado Perfeito?
por Molina » Qui Nov 25, 2010 17:00
- 6 Respostas
- 6695 Exibições
- Última mensagem por pedroaugustox47

Sex Mai 11, 2012 16:28
Desafios Difíceis
-
- Quadrado perfeito
por guillcn » Ter Abr 05, 2011 19:15
- 2 Respostas
- 2523 Exibições
- Última mensagem por guillcn

Ter Abr 05, 2011 19:54
Álgebra Elementar
-
- Ajuda com quadrado perfeito
por joaoalbertotb » Ter Ago 25, 2009 13:01
- 2 Respostas
- 2315 Exibições
- Última mensagem por joaoalbertotb

Qua Ago 26, 2009 12:20
Trigonometria
-
- Trinômio Quadrado Perfeito
por Balanar » Ter Ago 10, 2010 22:48
- 2 Respostas
- 4927 Exibições
- Última mensagem por DanielFerreira

Dom Jan 08, 2012 18:05
Desafios Difíceis
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
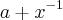 , a expressao
, a expressao  e igual a :
e igual a :
 para
para 
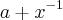 , a expressao
, a expressao  e igual a :
e igual a :
 para
para 



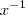 para o lado esquerdo da igualdade. Em seguida, eleve os dois ao quadrado, lembrando o produto notável
para o lado esquerdo da igualdade. Em seguida, eleve os dois ao quadrado, lembrando o produto notável 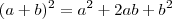 . Lembre-se também que
. Lembre-se também que 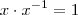 . Em seguida, isole
. Em seguida, isole 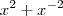 e veja que cairá onde eu cheguei. Refaça no papel que ficará mais claro.
e veja que cairá onde eu cheguei. Refaça no papel que ficará mais claro.

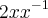 elimina-se o x pelo
elimina-se o x pelo 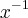 restando o +2.
restando o +2.


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
