 por renanrdaros » Sex Mar 25, 2011 18:27
por renanrdaros » Sex Mar 25, 2011 18:27

Resolvendo a expressão e analisando os dois casos possíveis, chego em uma inequação de 2º grau com \Delta<0
Como resolvo a partir daí? O resultado do livro não é vazio!
-
renanrdaros
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Mar 19, 2011 19:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. de Computação
- Andamento: cursando
 por LuizAquino » Sex Mar 25, 2011 18:31
por LuizAquino » Sex Mar 25, 2011 18:31
Envie a sua resolução para que possamos identificar onde está o problema.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por renanrdaros » Sex Mar 25, 2011 18:56
por renanrdaros » Sex Mar 25, 2011 18:56
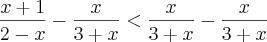

Multiplicando ambos os lados pelo denominador, simplificando e considerando os dois casos (denominador<0 e denominador>0), chego nas seguintes inequações:
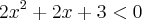
e

Elas não têm raízes reais. E a partir daí não sei resolver.
-
renanrdaros
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Mar 19, 2011 19:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. de Computação
- Andamento: cursando
 por MarceloFantini » Sex Mar 25, 2011 20:22
por MarceloFantini » Sex Mar 25, 2011 20:22
Vamos analisar assim:

. Como o numerador é sempre positivo, basta descobrir quando

é negativo.
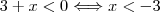

Assim,

.
Em questões assim, não elimine o denominador. Trabalhe com a fração.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por renanrdaros » Sáb Mar 26, 2011 01:52
por renanrdaros » Sáb Mar 26, 2011 01:52
Obrigado por mais essa!
-
renanrdaros
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Mar 19, 2011 19:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. de Computação
- Andamento: cursando
 por LuizAquino » Sáb Mar 26, 2011 10:31
por LuizAquino » Sáb Mar 26, 2011 10:31
renanrdaros escreveu:Multiplicando ambos os lados pelo denominador, simplificando e considerando os dois casos (denominador<0 e denominador>0), chego nas seguintes inequações:
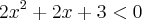
e

É comum os alunos cometerem o equívoco de multiplicar as inequações usando expressões e não se preocupar com o sinal das mesmas. Leia no tópico a seguir um comentário a respeito disso:
inequação, dúvida.viewtopic.php?f=106&t=3856
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por johnlaw » Dom Mar 27, 2011 13:08
por johnlaw » Dom Mar 27, 2011 13:08
Então, desenvolvendo o

eu chego em

. O denominador fica igual, mas não posso dizer que ele será maior que zero e então encontrar somente o denominador.
Desenvolvi assim:
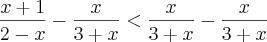


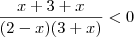
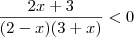
Para dar a equaçã de 2º grau acima, aquele primeiro +x (na 3ª linha desenvolvida) deveria ser -x, mas o que fiz está errado ?
Valeu! Abraços a todos!
-
johnlaw
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Ago 06, 2010 13:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática Licenciatura
- Andamento: cursando
 por johnlaw » Dom Mar 27, 2011 16:33
por johnlaw » Dom Mar 27, 2011 16:33
Ah sim!! OK Luiz, muito obrigado!
Abraços!
-
johnlaw
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Ago 06, 2010 13:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática Licenciatura
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (Equação de 2° grau) com o Delta sem valor exato
por morcego265 » Sáb Jul 27, 2013 13:48
- 1 Respostas
- 1517 Exibições
- Última mensagem por DanielFerreira

Sáb Ago 03, 2013 08:48
Equações
-
- [Inequação] Menor Inteiro Positivo
por CJunior » Qui Fev 06, 2014 21:37
- 2 Respostas
- 1933 Exibições
- Última mensagem por e8group

Qui Fev 06, 2014 22:30
Álgebra Elementar
-
- Função do 2° grau - o menor valor numa expressão
por PeterHiggs » Sex Mai 25, 2012 22:24
- 1 Respostas
- 2342 Exibições
- Última mensagem por PeterHiggs

Sáb Mai 26, 2012 16:09
Funções
-
- Inequação 2o grau
por guijermous » Sex Fev 26, 2010 14:29
- 3 Respostas
- 3728 Exibições
- Última mensagem por Molina

Sex Fev 26, 2010 18:00
Funções
-
- Inequação 1° grau
por Luiza » Sex Jul 16, 2010 10:14
- 1 Respostas
- 2750 Exibições
- Última mensagem por Tom

Sex Jul 16, 2010 12:34
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





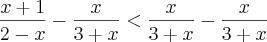

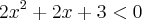


 . Como o numerador é sempre positivo, basta descobrir quando
. Como o numerador é sempre positivo, basta descobrir quando  é negativo.
é negativo.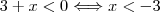

 .
.



 eu chego em
eu chego em  . O denominador fica igual, mas não posso dizer que ele será maior que zero e então encontrar somente o denominador.
. O denominador fica igual, mas não posso dizer que ele será maior que zero e então encontrar somente o denominador.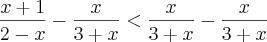


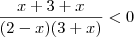
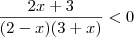

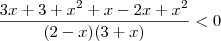
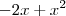 e não
e não  como você fez.
como você fez.

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)