 por rvitorper » Sex Mar 25, 2011 00:05
por rvitorper » Sex Mar 25, 2011 00:05
Resolva um triângulo ABC, sabendo que
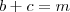
,

e  em que m, n e  são medidas conhecidas. (Ipsis literis do livro)
Não apresenta resposta no fim do livro. O que complica mais ainda.
Tudo certo ao ler o enunciado. Percebo que tenho que fazer

ficar em função de

. Daí tentei lei dos cossenos. Não vai. Lei dos senos não rola, falta B e C. Não encontrei nenhuma questão parecida em Lidski e o Google dá nenhum resultado. Não sei onde vai entrar

. Por favor ajudem-me!
-
rvitorper
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Mar 17, 2011 16:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Resolução de triângulos quaisquer.
por rodsales » Dom Nov 15, 2009 18:45
- 1 Respostas
- 6814 Exibições
- Última mensagem por Lucio Carvalho

Seg Nov 16, 2009 10:56
Trigonometria
-
- [Triangulos] Questão Unesp-93
por Ludmilla_Mayer » Seg Mar 10, 2014 22:31
- 3 Respostas
- 5542 Exibições
- Última mensagem por Ludmilla_Mayer

Seg Mar 17, 2014 12:20
Geometria Plana
-
- Questão envolvendo semelhança de triângulos
 por Anniemf » Qua Mai 23, 2012 20:55
por Anniemf » Qua Mai 23, 2012 20:55
- 1 Respostas
- 2051 Exibições
- Última mensagem por Cleyson007

Ter Mai 29, 2012 18:01
Geometria Plana
-
- [Semelhança de triângulos] Triângulos quadrados
 por Debora Bruna » Seg Ago 08, 2016 12:18
por Debora Bruna » Seg Ago 08, 2016 12:18
- 0 Respostas
- 1473 Exibições
- Última mensagem por Debora Bruna

Seg Ago 08, 2016 12:18
Geometria Plana
-
- Resolução de questão.
por Androcles Lima Souza » Sex Nov 27, 2009 13:37
- 0 Respostas
- 1597 Exibições
- Última mensagem por Androcles Lima Souza

Sex Nov 27, 2009 13:37
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
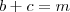 ,
,  e  em que m, n e  são medidas conhecidas. (Ipsis literis do livro)
e  em que m, n e  são medidas conhecidas. (Ipsis literis do livro) ficar em função de
ficar em função de  . Daí tentei lei dos cossenos. Não vai. Lei dos senos não rola, falta B e C. Não encontrei nenhuma questão parecida em Lidski e o Google dá nenhum resultado. Não sei onde vai entrar
. Daí tentei lei dos cossenos. Não vai. Lei dos senos não rola, falta B e C. Não encontrei nenhuma questão parecida em Lidski e o Google dá nenhum resultado. Não sei onde vai entrar  . Por favor ajudem-me!
. Por favor ajudem-me!

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.