Olá Danjr,
Você precisa desde já tomar muito cuidado com a maneira como ensina as coisas. Ainda mais sendo você um aluno de um curso de graduação em licenciatura.
Imagine que você ensinou essa técnica para um aluno e pediu para ele resolver o exercício: Determine as raízes da equação

.
Seguindo o que você ensinou, o aluno irá procurar dois números tais que a soma seja -5 e o produto seja 6. Daí, ele encontrará -2 e -3, já que (-2)+(-3)=-5 e (-2)(-3)=6. Ele muito provavelmente irá dizer que as raízes da equação são -2 e -3. O que está errado.
Muito provavelmente ele não irá montar a equação
(x-2)(x-3)=0 para daí poder determinar que as raízes são 2 e 3.
Além disso, ignorar o sinal no início do processo não configurou-se em vantagem, já que no final temos que trocar o sinal de qualquer maneira se quisermos descobrir as raízes verdadeiras.
Eu acredito que esse processo possa confundir mais do que ajudar o aluno.




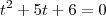 você quer encontrar dois números tais que a soma seja
você quer encontrar dois números tais que a soma seja 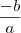 e uso o valor de "b".
e uso o valor de "b". .
.
 .
.



