Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por Mechanic » Sex Mar 18, 2011 21:00
por Mechanic » Sex Mar 18, 2011 21:00
João sai de Coimbra, viajando a velocidade constante. Passa por um marco que contém dois algarismos. Uma hora depois passa por outro marco, contendo os dois mesmos algarismos, mas por ordem inversa. Uma hora depois passa por um terceiro marco, contendo os mesmos algarismos, separados por um zero.
Qual é a velocidade a que vai?
P.S.: os números dos marcos são:
25 52 502 205
-
Mechanic
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Mar 18, 2011 20:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Sáb Mar 19, 2011 16:08
por MarceloFantini » Sáb Mar 19, 2011 16:08
Mechanic, onde arranjou a questão?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Mechanic » Sáb Mar 19, 2011 16:34
por Mechanic » Sáb Mar 19, 2011 16:34
Esta pergunta é de um desafio do meu livro de matemática B do 10ºano
-
Mechanic
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Mar 18, 2011 20:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Fabricio dalla » Qua Mar 23, 2011 00:13
por Fabricio dalla » Qua Mar 23, 2011 00:13
e o estranho que a variaçao de espaço entre os marcos deveria ser o msm pois tempo é.
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Qua Mar 23, 2011 00:30
por MarceloFantini » Qua Mar 23, 2011 00:30
Exatamente.
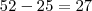
, logo isso significaria que, com velocidade constante, esta seria de

. Porém, com isso, é
impossível que em uma hora ele passasse no marco 502 (supondo a mesma estrada).
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Desafios Médios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- quantos dias durou a viagem
por sinuca147 » Seg Mai 18, 2009 03:43
- 6 Respostas
- 6916 Exibições
- Última mensagem por Neperiano

Seg Mai 18, 2009 18:39
Álgebra Elementar
-
- que dificil
por giboia90 » Seg Abr 08, 2013 03:34
- 1 Respostas
- 1468 Exibições
- Última mensagem por anabatista

Ter Abr 09, 2013 01:37
Estatística
-
- Primitiva difícil
por photon » Sáb Set 19, 2009 18:39
- 0 Respostas
- 1450 Exibições
- Última mensagem por photon

Sáb Set 19, 2009 18:39
Cálculo: Limites, Derivadas e Integrais
-
- questão dificil.
por natanskt » Seg Dez 13, 2010 18:20
- 1 Respostas
- 2448 Exibições
- Última mensagem por Molina

Sáb Dez 25, 2010 20:28
Binômio de Newton
-
- Questão dificil
por cortelettirlz » Qua Set 07, 2011 15:32
- 1 Respostas
- 1606 Exibições
- Última mensagem por MarceloFantini

Dom Set 11, 2011 19:43
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





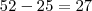 , logo isso significaria que, com velocidade constante, esta seria de
, logo isso significaria que, com velocidade constante, esta seria de  . Porém, com isso, é
. Porém, com isso, é ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.