Santa Lucci escreveu:Por exemplo, a função
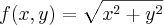
. Ao fazer as curvas de nível (o método que o Guidorizzi apresenta), teremos várias circunferências; a função, porém, assemelha-se mais a um plano com um bico do que a um paraboloide. Esse é um exemplo simplório, claro, mas me pergunto sobre como irei detectar esse tipo de comportamento?
Não há nada de "plano com um bico" no gráfico dessa função. Vejamos o seu gráfico para
x e
y no intervalo [-4, 4]:

- grafico-funcao.png (13.72 KiB) Exibido 2313 vezes
Como você disse, fazendo cortes paralelos ao eixo
xOy (isto é, fixando
z=r, com
r não nulo e positivo nesse caso) teremos circunferências, já que de
f(x, y) = r obtemos a equação

.
Se
x=0 (isso significa a interseção do gráfico com o plano
yOz), então temos o gráfico da função modular
z=|y|. O mesmo acontece para
y=0 (interseção do gráfico com o plano
xOz), quando teremos
z=|x| . Ambos os gráficos tem o formato da letra "V", com o vértice fixado na origem.
Por outro lado, fazendo cortes paralelos ao plano
yOz (o que significa fixarmos
x=r, com
r não nulo) temos
f(r, y) = z, de onde obtemos hipérboles
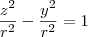
(apenas a parte positiva da mesma).
De modo semelhante, fazendo cortes paralelos ao plano
xOz (o que significa fixarmos
y=r, com
r não nulo) temos
f(x, r) = z, de onde obtemos hipérboles
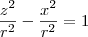
(apenas a parte positiva da mesma).
Veja que não tem jeito: você vai precisar dos conteúdos de Geometria Analítica. Por isso, recomendo que faça uma revisão sobre o assunto.
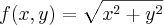 . Ao fazer as curvas de nível (o método que o Guidorizzi apresenta), teremos várias circunferências; a função, porém, assemelha-se mais a um plano com um bico do que a um paraboloide. Esse é um exemplo simplório, claro, mas me pergunto sobre como irei detectar esse tipo de comportamento?
. Ao fazer as curvas de nível (o método que o Guidorizzi apresenta), teremos várias circunferências; a função, porém, assemelha-se mais a um plano com um bico do que a um paraboloide. Esse é um exemplo simplório, claro, mas me pergunto sobre como irei detectar esse tipo de comportamento?

 .
.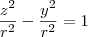 (apenas a parte positiva da mesma).
(apenas a parte positiva da mesma).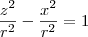 (apenas a parte positiva da mesma).
(apenas a parte positiva da mesma).

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.