 por vinik1 » Ter Mar 08, 2011 20:08
por vinik1 » Ter Mar 08, 2011 20:08
Sou novo no forúm, e novato na matematica também, comecei o curso de engenharia elétrica esse ano, e preciso estar afiado em conceitos básicos da matemática portanto minhas dúvidas são bem simples, mas importantes!
Ai vai:
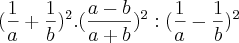
O resultado disso vai dar 1.. eu fiz.. refiz.. tentei fazer de novo... e nao consegui chegar a 1! Estou errando em algo bem bobo, mas preciso descobrir onde..
Bom.. vamos por partes..
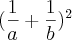
=

Certo?
Se estiver certo passamos para o próximo passo..
-
vinik1
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Ter Mar 08, 2011 19:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia elétrica
- Andamento: cursando
 por vinik1 » Ter Mar 08, 2011 22:49
por vinik1 » Ter Mar 08, 2011 22:49
Desculpa minha ignorância.. mas eu não intendi o que vc fez..
No segundo passo:
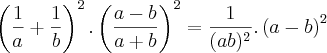
????????????
Como assim?
Poderia me explicar?
O correto não seria eu fazer
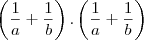
antes ??
aplicando a distributiva fica
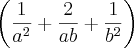
?
Não? Tá errado? Pq?
Ah! muito obrigado pelo link! vai me ajudar bastante
-
vinik1
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Ter Mar 08, 2011 19:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia elétrica
- Andamento: cursando
 por vinik1 » Qua Mar 09, 2011 14:15
por vinik1 » Qua Mar 09, 2011 14:15
Daonde surgiu esse 1 no numerador?
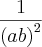
Pq é errado fazer
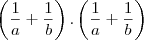
?
-
vinik1
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Ter Mar 08, 2011 19:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia elétrica
- Andamento: cursando
 por MarceloFantini » Qua Mar 09, 2011 14:28
por MarceloFantini » Qua Mar 09, 2011 14:28
Faça o MMC da soma e você verá de onde surgiu o

. E não é errado, apenas não facilita o seu trabalho. Vou fazer do jeito que você quer e verá que é a mesma coisa:

Multiplicando o primeiro no numerador e denominador por
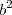
, o segundo por

e o terceiro por

:
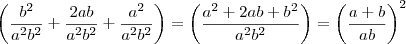
Veja que é a mesma coisa, por muito menos trabalho.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por vinik1 » Qua Mar 09, 2011 16:38
por vinik1 » Qua Mar 09, 2011 16:38
Muito bem.. as coisas estão se esclarecendo..

Aplicando a distributiva fica:
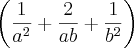
Fazendo o MMC e igualando os denominadores fica:

Até ai td bem.. mas para simplificar isso eu estou errando:

Não posso cancelar

e
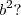
ficando apenas 2ab? porquê? Qual a melhor maneira de simplificar a partir daí?
-
vinik1
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Ter Mar 08, 2011 19:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia elétrica
- Andamento: cursando
 por MarceloFantini » Qua Mar 09, 2011 17:02
por MarceloFantini » Qua Mar 09, 2011 17:02
Não, pra cancelar você teria que ter

como fator comum no numerador, que não acontece. A melhor maneira de simplificar é o que eu fiz: usar produto notável em sim e deixar tudo como uma fração ao quadrado.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por vinik1 » Qua Mar 09, 2011 17:56
por vinik1 » Qua Mar 09, 2011 17:56
O que é produto notável?
Se fosse

no denominador poderia cancelar?
Por exemplo:
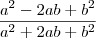
Como simplificar? Nesse caso pode cancelar
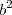
e

?
-
vinik1
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Ter Mar 08, 2011 19:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia elétrica
- Andamento: cursando
 por MarceloFantini » Qua Mar 09, 2011 23:40
por MarceloFantini » Qua Mar 09, 2011 23:40
Não. Produto notável são produtos comuns, por exemplo

,

, etc. Você só poderia cancelar se a fração fosse assim:

Note que no numerador

é fator comum, colocando em evidência poderíamos cancelar.
Em outras palavras, você só pode cancelar se o mesmo elemento que estiver no numerador estiver no denominador, e estiver fatorado no numerador.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por vinik1 » Sex Mar 11, 2011 01:06
por vinik1 » Sex Mar 11, 2011 01:06
]Ah sim! Ficou claro porém, não estou conseguindo chegar ao resultado fazendo a multiplicação dos parênteses.
Eu sei que é a maneira mais difícil, mas eu quero descobrir onde estou errando.
por Ex:
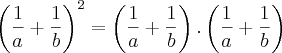
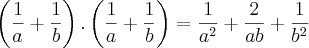
Muito bem.. agora fazendo a soma da fração com o MMC dos denominadores fica:
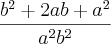
CERTO? certo..
Agora o outro parênteses

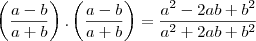
CERTO? certo..
PORTANTO

é o mesmo que
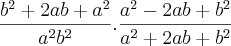
CERTO?
certo?
Onde foi que eu errei? Se estiver certo.. como fazer essa multiplicação?
-
vinik1
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Ter Mar 08, 2011 19:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia elétrica
- Andamento: cursando
 por vinik1 » Sex Mar 11, 2011 15:57
por vinik1 » Sex Mar 11, 2011 15:57
CERTO!
Muito obrigado!
duvida resolvida
-
vinik1
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Ter Mar 08, 2011 19:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia elétrica
- Andamento: cursando
 por vinik1 » Sáb Mar 12, 2011 12:27
por vinik1 » Sáb Mar 12, 2011 12:27
Nesse caso posso considerar

como fator, pois está multiplicando

??

Ficamos com
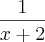
?
-
vinik1
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Ter Mar 08, 2011 19:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia elétrica
- Andamento: cursando
 por vinik1 » Sáb Mar 12, 2011 13:24
por vinik1 » Sáb Mar 12, 2011 13:24
mais uma:

é igual a
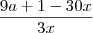
????
-
vinik1
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Ter Mar 08, 2011 19:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia elétrica
- Andamento: cursando
 por MarceloFantini » Sáb Mar 12, 2011 18:17
por MarceloFantini » Sáb Mar 12, 2011 18:17
Vinik, por favor evite colocar mais de uma dúvida num tópico.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- frações algebricas
por tamirosa » Qui Out 29, 2009 20:11
- 1 Respostas
- 3309 Exibições
- Última mensagem por Molina

Sex Out 30, 2009 11:37
Álgebra Elementar
-
- Frações Algébricas
por LuizCarlos » Dom Ago 07, 2011 21:45
- 5 Respostas
- 2933 Exibições
- Última mensagem por MarceloFantini

Seg Ago 08, 2011 02:06
Álgebra Elementar
-
- Frações Algébricas
por LuizCarlos » Qui Abr 19, 2012 14:33
- 4 Respostas
- 2195 Exibições
- Última mensagem por LuizCarlos

Qui Abr 19, 2012 17:59
Álgebra Elementar
-
- Frações Algébricas Ajudem-me!
por Jansen » Seg Ago 31, 2009 23:32
- 0 Respostas
- 1675 Exibições
- Última mensagem por Jansen

Seg Ago 31, 2009 23:32
Sistemas de Equações
-
- Dúvida em frações algébricas
por LuizCarlos » Dom Abr 22, 2012 10:04
- 7 Respostas
- 3243 Exibições
- Última mensagem por DanielFerreira

Qui Abr 26, 2012 20:14
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
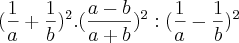
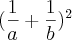 =
=  Certo?
Certo?

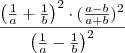

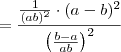
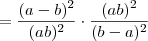
![= \frac{(a-b)^2}{(ab)^2} \cdot \frac{(ab)^2}{[(-1)(a-b)]^2} = \frac{(a-b)^2}{(ab)^2} \cdot \frac{(ab)^2}{[(-1)(a-b)]^2}](/latexrender/pictures/67e05c1962e0f06208e0b108dfe649e7.png)
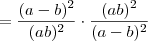

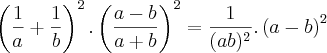 ????????????
????????????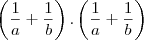 antes ??
antes ?? 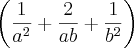 ?
?
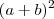 no denominador da multiplicação.
no denominador da multiplicação.
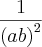
 . E não é errado, apenas não facilita o seu trabalho. Vou fazer do jeito que você quer e verá que é a mesma coisa:
. E não é errado, apenas não facilita o seu trabalho. Vou fazer do jeito que você quer e verá que é a mesma coisa:
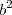 , o segundo por
, o segundo por  :
: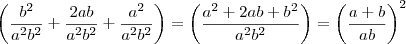


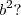 ficando apenas 2ab? porquê? Qual a melhor maneira de simplificar a partir daí?
ficando apenas 2ab? porquê? Qual a melhor maneira de simplificar a partir daí? como fator comum no numerador, que não acontece. A melhor maneira de simplificar é o que eu fiz: usar produto notável em sim e deixar tudo como uma fração ao quadrado.
como fator comum no numerador, que não acontece. A melhor maneira de simplificar é o que eu fiz: usar produto notável em sim e deixar tudo como uma fração ao quadrado. no denominador poderia cancelar?
no denominador poderia cancelar?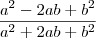
 ,
,  , etc. Você só poderia cancelar se a fração fosse assim:
, etc. Você só poderia cancelar se a fração fosse assim:
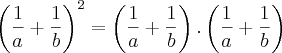
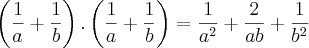
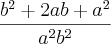

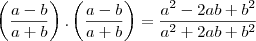

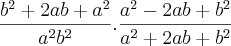
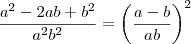
 como fator, pois está multiplicando
como fator, pois está multiplicando  ??
??
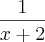

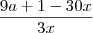
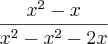
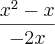
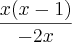
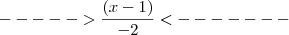



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.