Pessoal, gostaria de confirmar se minhas respostas estão corretas, por favor, me ajudem!

pela forma de substituição daria

pela forma de fatoração ficaria
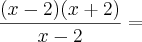 ? x=2 e
? x=2 e e)

f)
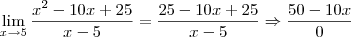 ou seja, o denominador =0.O que eu faço aqui, please? rsrs
ou seja, o denominador =0.O que eu faço aqui, please? rsrsAs outras estão corretas?
Muito obrigado pela ajuda!


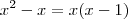



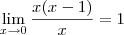
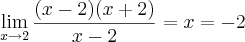
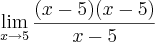 aqui zera.
aqui zera. seria isto?
seria isto?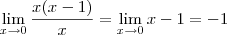
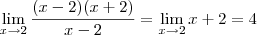

 e
e  , sendo
, sendo 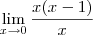 é o mesmo que
é o mesmo que 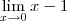 .
.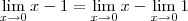 .
.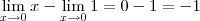 .
.![\lim_{x\rightarrow10}\left[1n(10-x) \right] \lim_{x\rightarrow10}\left[1n(10-x) \right]](/latexrender/pictures/45e72c2c793aa426ccced41f835107e8.png)

 e tente responder o exercício.
e tente responder o exercício.
 .
.
 :
: