Ai vai:
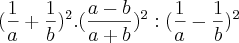
O resultado disso vai dar 1.. eu fiz.. refiz.. tentei fazer de novo... e nao consegui chegar a 1! Estou errando em algo bem bobo, mas preciso descobrir onde..
Bom.. vamos por partes..
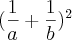 =
=  Certo?
Certo?Se estiver certo passamos para o próximo passo..


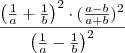

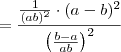
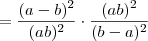
![= \frac{(a-b)^2}{(ab)^2} \cdot \frac{(ab)^2}{[(-1)(a-b)]^2} = \frac{(a-b)^2}{(ab)^2} \cdot \frac{(ab)^2}{[(-1)(a-b)]^2}](/latexrender/pictures/67e05c1962e0f06208e0b108dfe649e7.png)
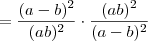

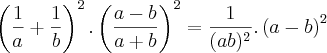 ????????????
????????????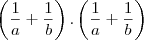 antes ??
antes ?? 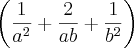 ?
?
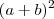 no denominador da multiplicação.
no denominador da multiplicação.
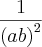
 . E não é errado, apenas não facilita o seu trabalho. Vou fazer do jeito que você quer e verá que é a mesma coisa:
. E não é errado, apenas não facilita o seu trabalho. Vou fazer do jeito que você quer e verá que é a mesma coisa:
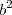 , o segundo por
, o segundo por  :
: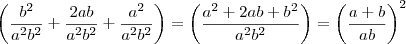


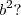 ficando apenas 2ab? porquê? Qual a melhor maneira de simplificar a partir daí?
ficando apenas 2ab? porquê? Qual a melhor maneira de simplificar a partir daí? como fator comum no numerador, que não acontece. A melhor maneira de simplificar é o que eu fiz: usar produto notável em sim e deixar tudo como uma fração ao quadrado.
como fator comum no numerador, que não acontece. A melhor maneira de simplificar é o que eu fiz: usar produto notável em sim e deixar tudo como uma fração ao quadrado. no denominador poderia cancelar?
no denominador poderia cancelar?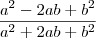
 ,
,  , etc. Você só poderia cancelar se a fração fosse assim:
, etc. Você só poderia cancelar se a fração fosse assim:
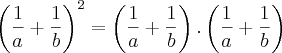
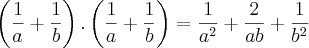
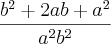

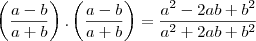

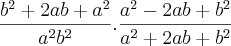
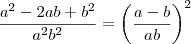
 como fator, pois está multiplicando
como fator, pois está multiplicando  ??
??
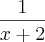

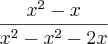

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)